Имеет место следующая теорема.

Теорема: последовательность X^(m)=(X₁^(m)…X_n^(m))ÎRⁿ m=1,2…n сходилась к точке X=(X_1,…Xn) чтобы

Опр.9: Последовательность точек X^mÎRⁿ m=1,2,…называется ограниченной, если множество её значений, т.е.(X^m:m=1,2,…) ограничено в пространстве Rⁿ

Теорема Больцако-Вейештрассе: Из любой ограниченной последовательности точек пространства Rⁿ можно выделить сходящуюся последовательность.

Опр.10: Пусть Е – некоторое множество точек евклидова пространства XÎE Точка XÎE называется внутренней точкой множества (относительно пространства Rⁿ), если существует e-окрестность этой точки, содержащаяся во множестве Е, т.е. существует такое e > 0, число U(x,e)ÌE.

Опр.11: Множество, каждая точка которого является его внутренней точкой (относительно рассматриваемого пространства Rⁿ), называется открытым множеством.

Лема: Всякая e-окрестность U(x,e) любой точки XÎRⁿ является открытым множеством.

Лема: Пересечение конечного числа, также как объединение любой совокупности открытых множеств является открытыми множествами.

Н-р {-1/n,…1+1/n} Бесконечное число пересекаемых таких множеств [0,1] – замкнутое множество.

Опр.12: Всякое открытое множество содержащее точку C называется её окрестностью: U(X)

Опр.13: Точка C ÎRⁿ называется точкой прикосновения множества EÌRⁿ, если любая окрестность этой точки содержит по крайней мере одну точку множества Е. Очевидно каждая точка множества Е является его точкой прикосновения ибо всякая окрестность тXÎE содержит саму точку C. Вместе с тем могут существовать и точки прикосновения данного множества, не принадлежащие ему (н-р интервала на прямой является его ………… прикосновения).

Опр.14: Если у точки C ÎE существует окрестность не содержащая ни каких других точек множества Е, кроме самой точки, то эта точка называется изолированной точкой множества Е.

Опр.15: Т. х принадлежит Rn наз. предельной т. множества Е, если любая окрестность т. х содержащий покрайне мере одну т. множ-ва,относительно оси х

Очевидно что предельная точка явл. т. проникновения

Примеры n=1 E=]0,1[ каждая т. [0,1] явл. точкой прикосновения и предельной точкой мн-ва Е, при этом 0,1 не принадлежат Е.

Е=]0,1[U{2} т. 2- изолированная точка, мн-ва точек прикосновения [0,1]U{2}

Т.(2) –т. прикосновения но не придельная.

Опр.16: Совокупность всех точек прикосновения мн-ва ЕСRn наз. Замыканием мн-ва Е и обозначается Е.

Опр.17: Мн-во Е наз. Замкнутым если Е = Е,т.е. если она содержит все свои точки прикосновения

n=1 ]0,1[ не явл. замкнутым

[0,1] – замкнутое мн-во

Мн-во Е замкнуто т и т.т. когда оно содержитоси свои предельные точки.

Опр.18: Для всякого ЕсRn мн-во Rn\E наз.его дополнением в прастранстве Rn

Лемма: Для того чтобы мн-во было открытым необходимо и достаточно,чтобы его дополнение было замкнутым.

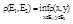
Опр.19: Для 2-х мн-вЕ1 иЕ2 величина

Наз. Растоянием между Е1 и Е2

Лемма: Если 2-а замкнутых множества не пересекаются и покрайнемере одно из них ограничено, то расстояние между ними положительно.

Опрд.20: Т. х принадлежащая Rn наз. граничной т. мн-ва Е принадлежащего Rn если в любой её окрестности существует точки как принадлежащие мн-ву Е, так и не принадлежащие ему. Совокупность всех ограниченных точекмн-ва Е наз.его границей и обозначается ¶Е, очевидно ¶ЕсЕ.

Прмеры Е=Q2 –замкнутый круг любая точка окружности

Опред.21: Мн-во точек х=(x1… xn) пр-ва Rn, координаты корых заданы как непри-

рывные фун. хi = хi(t) Где i =1,2…n определённые на некотором отрезке [a,b] наз.

неприрывной кривой в пространстве Rn t – параметр,т. х(а) - начало,х(b) – конец

данной кривой.

Опред.22: Мн-во Е c Rn, любые 2-е точки,которые можно соединить целиком лежащие в нём неприрывной кривой наз. связным(линейно связным

П-р: отрезок.

Опред.23: Открытое линейно-связонное множество наз. облостью

П-р: n=1 всякий интервал область

n=2 2-а не пересекающихся круга – не явл областью

Опред.24: Мн-во, лежащие в Rn не являющееся замкнутым некоторой облости, наз.

Замкнутой облостью

Опред.25: Мн-во А сRn наз. …. Если из любой плоскости его точек можно

Выделить сходящиюся ….., предел которой пренодлежит А.

Теорема: Для ого чтобы мн-во Е пренадлежащие Rn было компоктным

необходимо и дстаточно чтобы оно было ограниченным и замкнутым.

Если 2-а замкнутых мн-ва не пересекаются и покрайне мере одно из них …,то

расстояние между ним больше нуля.

Опр.26: М н-во точек х=(x1… xn) пр-ва Rn координаты которых представимы в

виде Xi = Xi + αi t, где i =1,2…n, -∞ < t < + ∞, ∑αi 2 ≠ 0 наз. прямой в пр-ве с Rn

проходящей через точку х˚.

Не нашли, что искали? Воспользуйтесь поиском: