Предел функции. Непрерывность функции. Свойства непрерывных функций.

Опр.1: Пусть функция f определена на множестве , Е некоторое подмножества множества , 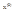-это предельная точка множества Е. Число А – называется пределом функции f по множеству Е в точке х⁽⁰⁾, если для любой последовательности точек , при , такой что: 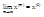числовая последовательность сходится к числу А.

Обозначение:

Опр.2: Пусть функция f определена на множестве , Е некоторое подмножества множества , 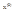-это предельная точка множества Е. Число А – называется пределом функции f по множеству Е в точке х⁽⁰⁾, если для каждого Е>0 такое , что для каждой точки , , для которой 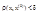выполняется неравенство:

Аналогично случаю n=1 доказывается эквивалентность этих определений для любых n.

Проколотая окрестность __________________

Опр.3: Если функция f определена в некоторой проколотой окрестности точки х⁽⁰⁾ под пределом функции в точке х⁽⁰⁾ по этой проколотой окрестности называется просто предел функции в точке, и обозначается:

Опр.4: Пусть через точку х⁽⁰⁾ проведена прямая l, - некоторая проколотая окрестность точки (х⁽⁰⁾), предел функции f в точке х⁽⁰⁾ по пересечению называется пределом функции f в точке х⁽⁰⁾ в направлении прямой l.

Опр.5: Если множество Е является множеством точек, некоторой кривой, проходящей через точку х⁽⁰⁾, то в этом случае предел функции f п множеству Е при называется пределом функции по данной кривой.

Очевидно, что если 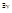функции f предел в точке х⁽⁰⁾, то он существует в этой точке и по любому направлению и по любой кривой, причем эти пределы совпадают.

Пример:

, определить во всех точках _________, кроме точки(0,0)

Исследуем поведение этой функции по различным направлениям и найдем пределы в точке (0,0).

Уравнение прямой, проходящей через начало координат по направлению вектора с координатами , имеет вид: причем

Тогда:

Т.е. предел существует по любому направлению и равен нулю.

Теперь:

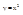
Вывод: предел в точке (0,0) не существует.

Аналогичным случаю одной переменной для функции многих переменных по множеству имеют место соответствующие теоремы о пределах сумм, произведений, частного. Наряду с рассмотренными пределами функции многих переменных можно рассмотреть и пределы других видов, связанные с последовательным переходом пределов.

или такие пределы называются повторными.

Пример:

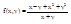, интересует точка (0,0)

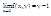
Рассмотрим второй предел:

;

повторные пределы могут быть неравны.

Пример:

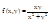
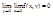и

- не существует так как по прямой х=0 или y=0 предел равен 0, а по прямой y=х – предел равен ½, поэтому предел по множеству в точке (0,0) не существует.

Таким образом из одного лишь существования предела функции в данной точке не следует существование повторных пределов и наоборот.

Теорема: Пусть функция f(x,y) определена на множестве Е, содержащим все точки прямоугольной окрестности:

, точки (x₀,y₀),кроме может быть прямых: 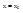и , если существует предел функции по множеству Е, и при любом при

, о повторные предел 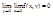- существует и это предел равен пределу по множеству то есть:

Не нашли, что искали? Воспользуйтесь поиском: