Непрерывность функции.

Опр.1: Функция f определена на множестве 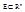называется непрерывной в точке 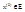если:

-

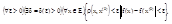
Замечание: Из определения следует, что в изолированной точке 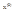является предельной точкой для множества Е, то данное определение непрерывности функции f в точке 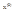по множеству Е эквивалентно условию:

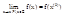
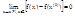
приращение: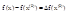

Тогда получаем:

;

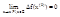Значит:

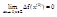
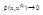В имеем или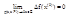

Аналогично случаю n =1, доказываются, что если функции f и g непрерывны в точке x⁽⁰⁾множества Е то функции: f + g, f - g, fg, f/g, при g(x) не равное 0, также непрерывны в точке x⁽⁰⁾.

Для функции: f(x₁,x₂,...x_n) при n строго больше 1, наряду с непрерывностью в выше указанном смысле, которую называют непрерывностью по совокупности переменных, можно рассматривать и непрерывность по отдельным переменным.

Не нашли, что искали? Воспользуйтесь поиском: