Метод множителей Логранжа для нахождения точек условного экстремума

Пусть ф-ции f₀,f₁…f_m непрер диф-мы в откр множ GÎRⁿ

Теорема 1: Пусть х⁽⁰⁾ точка условного экстремума ф-ции f₀ при выполнении ур-ий связи (3), тогда в этой точке Ñf₀,Ñf₁…Ñf_m – линейно зависимы, т.е. существуют не все равные 0

числа l0, l1…lm, такие что:

Следствие: Если в т.х⁰ условного экстремума фун.fo относительно уравнения связи (3) Ñf1…Ñfm линейнонезависемых, то сущ. числа

l1… l m, такие что в этой точке: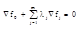

В координатной форме это условие для любых i=1,n в т. х⁰ имеет вид:

Где (*) l1… lm - удовлетворяют условию (7) называется фун. Лагранжа (*), рассматриваемой задачи сами числа l1…lm – называется множителями Лагранжа

Условие (7) означает что если т. х⁰ является т. условного экстремума фун. fo при выполнении уравнеий связи (3), то она явл- ся стационарной точкой для фун. Лагранжа, т.е.

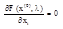
Где i =1,2…n

Будем выбирать l1… lm такими чтобы выполнялись условия (7). Для отыскания точки условного экстремума следует рассмотреть систему n+m урав-ний(3) и (7), относительно неизвестных x1⁰… xn⁰, l1… lm;

Достаточное условие следует из следуйщей Теоремы:

Если х⁰=(x1⁰… xn⁰) удовлетворяют уравнению связи и явл. стационарной точкой для фун Лагранжа и если 2-й деффе-л фун. Лагранжа в этой точке явл. положительным (отриццательнным) определённый квадратной формой относительно переменных dx1…dxn при условии, что они удовлетворяют системе:

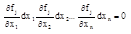
Где i =1,2…n

То т. х⁰ явл. т. условного экстремума min(max), для f относительно уравнения связи (3)

Не нашли, что искали? Воспользуйтесь поиском: