Пространственные частоты

Глава 1

ЛИНЕЙНЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ

Плоская монохроматическая световая волна.

Пространственные частоты

В качестве исходных приближений для теоретического исследования явлений, связанных с распространением и взаимодействием света с различными объектами, обычно используют волны наиболее простого вида, а именно плоские монохроматические волны. Волна называется плоской, если ее амплитуда и фаза в любой момент времени постоянны вдоль плоской поверхности, перпендикулярной направлению распространения волны (эта поверхность называется волновой или фазовой поверхностью). Характерным признаком плоской волны является также постоянство направления ее распространения.

Понятие плоской монохроматической волны значительно облегчает описание и изучение волновых процессов. Выбор плоских монохроматических волн в качестве исходных объектов обусловлен не только их простотой, но и тем, что в целом ряде физических задач реальные волны можно приближенно рассматривать как плоские монохроматические. Такой выбор обусловлен и тем, что, в соответствии с принципом суперпозиции, общее решение волнового уравнения можно представить в виде линейной комбинации плоских монохроматических волн. Последнее утверждение следует из линейности волнового уравнения. Кроме того, по теореме Фурье любая физически реализуемая функция может быть выражена через совокупность гармонических функций с определенными частотами, амплитудами и начальными фазами.

Следует отметить, что реальные световые волны плоскими монохроматическими не являются. Однако любую реальную волну можно представить как суперпозицию плоских монохроматических волн, частоты и волновые числа которых непрерывно заполняют интервалы шириной соответственно D w и D k. Замена же суперпозиции волн одной плоской монохроматической волной допустима лишь в некоторых конкретных случаях и при определенных оговорках.

Среди различных решений волнового уравнения имеется простейшее решение вида

(1.1)

где

k×r = k_x x + k_y y + k_z z,

k_x, k_y, k_z – компоненты волнового вектора k. При этом должно выполняться соотношение

Формула (1.1) описывает плоскую монохроматическую световую волну, распространяющуюся в направлении, определяемом волновым вектором k. Такая волна создается гармоническими колебаниями источника, расположенного в плоскости r = 0. Формула (1.1) показывает, что в плоской монохроматической волне зависимость компоненты вектора E от радиус-вектора r и времени t выражается гармонической функцией. Здесь E ₀₀ – амплитуда волны, аргумент косинуса, т.е. функция 𝜑(r, t) = ωt – k ⋅ r + 𝛼 – фаза волны, 𝛼 = 𝜑(0, 0) – начальная фаза волны. Для какой-либо конкретной плоскости r = r ₁ начальной фазой называют величину 𝜑(r ₁) = Отметим, что фаза световой волны является одной из важнейших ее характеристик, определяющей результат взаимодействия когерентных световых волн друг с другом. Скалярное произведение k×r, как и любое число, является величиной, не зависящей от ориентации координатных осей. А это и означает, что формула (1.1) описывает плоскую монохроматическую волну, распространяющуюся в произвольном относительно данной системы отсчета направлении (произвольна ориентация вектора n = k / k по отношению к координатным осям). Функция (1.1) является простейшим решением волнового уравнения.

Зафиксируем какое-либо значение фазы

w t – k×r + 𝛼 = C = const (1.2)

Отсюда видно, что каждому значению времени t соответствует определенное значение радиус-вектора r, т.е. плоскость k×r = = w t + 𝛼 – C, перпендикулярная вектору k. Это соотношение показывает, что фазовую (или волновую) поверхность световой волны можно определить как геометрическое место точек, в которых в рассматриваемый момент времени фаза волны имеет одно и то же значение, или как геометрическое место точек, в которых колебания светового вектора Е происходят в одной фазе. Из соотношения (1.2) видно также, что фазовая плоскость перемещается в пространстве вдоль направления вектора k со скоростью 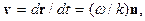где 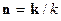– единичный вектор в направлении распространения волны . Скорость перемещения поверхности постоянной фазы в пространстве называется фазовой скоростью волны. Расстояние, на которое перемещается волновая поверхность за время, равное одному периоду колебаний светового поля, равно длине световой волны 𝜆.

Монохроматическая световая волна вида (1.1) является периодической как во времени, так и в пространстве. Временным периодом световой волны является период колебаний светового поля в волне, равный периоду колебаний источника Т. Пространственным периодом монохроматической волны является длина волны 𝜆. Поэтому длину световой волны можно определить как расстояние между двумя ближайшими точками в волне, в которых колебания светового поля происходят в одинаковой фазе (с разностью фаз, равной или кратной 2𝜋). Длина волны, в отличие от ее периода и частоты, задаваемых колебанием источника волн, различна в разных средах, так как в разных средах различна скорость света v. Поэтому длина волны в среде с показателем преломления определится как

l = 2 p v / w = (2 p c / w) / n.

Здесь 2 p c / w = l ₀ – длина волны света в вакууме. Следовательно,

l = l ₀ / n

Так как n > 1, то l < l ₀, причем, чем больше показатель преломления среды, тем более коротковолновым в этой среде является свет.

При математическом описании волновых явлений удобно использовать комплексную форму записи волны. В соответствии с формулой Эйлера

cos j ± i sin j = exp (± ij)

и, следовательно,

cos j = Re {exp(± ij)},

где i = – мнимая единица. С учетом этого функцию (1.1) можно представить в виде действительной части комплексной функции

E (r. t) = E ₀₀ exp [– i (w t ± k×r + 𝛼)],

где, исходя из соображений удобства, перед показателем степени экспоненты взят знак минус. Отметим, возможность использования комплексной формы записи обусловлена линейностью волнового уравнения. Представим это выражение в виде произведения

E (r, t) = E ₀ exp (± i k×r) × exp (–iw t). (1.3)

Формула (1.3) записана для волны, распространяющейся вдоль вектора k > 0 (при верхнем знаке в показателе первой экспоненты) и k < 0 (при нижнем знаке). Величину

E (r) = E ₀ e ^{± k×r} (1.4)

называют комплексной амплитудой плоской волны, распространяющейся в направлении k > 0 при знаке плюс в показателе экспоненты (перед произведением i k×r) и в направлении k < 0 – при знаке минус. Заметим, что в комплексном представлении формулы волн, распространяющихся в противоположных направлениях являются комплексно сопряженными друг другу (отличаются знаком перед i). Множитель E ₀ = = E ₀₀ exp (– i𝛼), определяющий как амплитуду E ₀₀, так и начальную фазу волны 𝛼, называют комплексной амплитудой в плоскости r = 0, т.е. E ₀ = E (0). Формула (1.4) позволяет определить поле плоской волны в любой плоскости r = = const > 0 или r = const < 0 по известному полю в плоскости r = 0, и наоборот. Фазовый множитель e ^{± k×r} определяет набег фазы kr плоской волны при ее распространении в свободном пространстве между двумя плоскостями, разделенными расстоянием r.

Комплексная амплитуда плоской волны в декартовой системе координат

E (x, y, z) = E ₀ exp [ i (k_x x + k_y y + k_z z)]. (1.5)

Отметим, что фаза колебаний светового поля в плоской волне является линейной функцией координат x, y, z. В плоскости z = = 0 плоская волна с такой амплитудой создает распределение поля

E (x, y, 0) = E ₀ exp [ i (k_x x + k_y y)].

В случае волны, распространяющейся вдоль оси Z, E (x, y, 0) = = E ₀ = const.

Комплексная амплитуда плоской волны имеет тот же физический смысл, что и комплексная амплитуда колебаний, но в отличие от последней содержит также множитель exp [ i (k_x x + k_y y + + k_z z)], определяющий зависимость фазы волны от пространственных координат. Физический смысл комплексности амплитуды связан с эллиптической поляризацией волны. Поверхность постоянной комплексной амплитуды представляет собой плоскость

k×r = k_x x + k_y y + k_z z = C = const,

перпендикулярную вектору k и отсекающую на осях координат X, Y, Z отрезки длиной C / k_x, C / k_y, C / k_z соответственно. Коплексная амплитуда плоской волны, распространяющейся вдоль оси Z, получается из амплитуды (1.5) как частный случай при k_x = k_y = = 0 и k_z = k. Пусть cos a, cos b, cos g – направляющие косинусы вектора n, а значит, и вектора k. Тогда

k_x = k cos a = (2 p / l) cos a, k_y = k cos b = (2 p / l) cos b,

k_z = k cos g = (2 p / l) cos g,

а комплексная амплитуда

E (x, y, z) = E ₀ exp (i k×r) =

= E ₀ exp . (1.6)

Выражение (1.6) содержит в явном виде все параметры волны (кроме частоты w): амплитуду E ₀, фазу и длину волны l = 2 p / k. Направление распространения волны задается направляющими косинусами cos a, cos b, cos g. Ориентация поля может быть задана, если рассматривать амплитуду волны как векторную величину.

Введем величины u, v. w, определив их как

u = k_x /2π = cosα/λ, v = k_y/2π = cos β / λ, w = k_z /2 π = cos γ /λ,

Эти величины называются пространственными частотами. С учетом этого формулу комплексной амплитуды плоской волны можно записать в виде

E (x, y, = E ₀ exp

Выражение 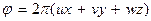определяет фазу плоской волны.

Пространственные частоты часто выражают через углы

j = p / 2 – a, q = p / 2 – b, f = p / 2 – g,

дополняющие направляющие углы a, b и g до p / 2. Тогда они записываются в виде

u = sin j / l, v = sin q / l, w = sin f / l.

Пространственные частоты связаны между собой очевидным соотношением поэтому зная какие-либо две пространственные частоты, можно найти третью пространственную частоту. Например, зная, u и v можно найти w:

При этом должно выполняться условие

Если ориентировать систему координат так, чтобы, например, волновой вектор волны лежал в плоскости XZ и составлял угол j с осью Z (рис. 1.1), то комплексная амплитуда такой волны будет иметь вид

E (x, z) = E ₀ exp [ i (x sin j + z cos j)]. (1.7)

Если волна раcпространяется вдоль оси Z, то k_x = k_y = 0, k_z = k, и тогда плоская гармоническая световая электромагнитная волна будет иметь вид

(1.8)

где верхний знак относится к волне, распространяющейся в положительном направлении оси Z, а нижний – в отрицательном направлении. Эта волна является решением одномерного волнового уравнения

(1.9)

В комплексной форме волна (1.13) запишется как

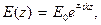(1.10)

где 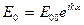– начальная комплексная амплитуда.

Плоская монохроматическая волна представляет собой синусоиду, имеющую бесконечную протяженность и длительность, т.е. не ограничена в пространстве и времени: – ¥ < t, z < ¥ (для

Рис. 1.1

волны, распространяющейся вдоль оси Z). Свойства ее в любой точке и в любой момент времени одинаковы: постоянны ее амплитуда, частота и начальная фаза. Плоская монохроматическая волна могла бы возбуждаться электрическими зарядами, совершающими бесконечно длительные гармонические колебания. В действительности же никакие реальные колебания не продолжаются бесконечно долго, все они имеют начало и конец. Следовательно, ограничены во времени и в пространстве и все реальные волны, а такие волны монохроматическими, а значит, и плоскими монохроматическими волнами не являются. Поэтому на практике под монохроматическими и, в частности, под плоскими монохроматическими волнами подразумевают волны, выражающиеся гармоническими функциями в конечном интервале времени и координат. Эти временные и пространственные интервалы должны быть много больше соответственно периода и длины волны. Чем лучше выполнены эти условия, тем с большим основанием можно пользоваться приведенными выше формулами плоских волн.

Не нашли, что искали? Воспользуйтесь поиском: