Линейные интегральные преобразования

В оптике

Интегральным преобразованием функции одной переменной f (x) (одномерным интегральным преобразованием) называют функцию F (x), определяемую интегралом вида

F (x) = ,

где K (x, x) – некоторая функция x и x, называемая ядром одномерного преобразования. Аналогично можно определить интегральное преобразование и функции двух переменных (двумерное интегральное преобразование):

F (x, h) = ,

где K (x, y; x, h) – ядро двумерного преобразования.

Интегральные преобразования играют большую роль в оптике. При помощи оптических систем можно получить любое такое преобразование. Применяя различные комбинации оптических элементов, можно задать функцию отклика оптической системы, являющуюся ядром интегрального преобразования K (x, y; x, h). Интегральные преобразования позволяют получить результаты более просто и с более высокой точностью даже в тех случаях, когда систему можно адекватно исследовать прямым методом. Согласно данному выше определению, все интегральные преобразования могут рассматриваться как линейные операторы, действующие на функцию f (x) (или на функцию f (x, y)) с целью получения функции F (x) (или функции F (x, h)). Следовательно, все используемые в оптике интегральные преобразования являются линейными. Кроме того, в оптике используются только такие интегральные преобразования, которые имеют обратное преобразование вида

f (x) = ,

или, в случае функции двух переменных,

f (x, y) = ,

где G (x, x) и G (x, y; x, h) – ядро обратного соответственно одномерного и двумерного преобразования. В некоторых случаях ядра прямого и обратного преобразований могут быть одинаковыми. Тогда функция и ее образ будут связаны симметричными соотношениями.

В оптике используются следующие интегральные преобразования: преобразование Фурье, преобразование Фурье – Бесселя, преобразование свертки, преобразование Френеля, преобразование Абеля, преобразование Гильберта, преобразование Мелина, преобразование Дирака и преобразование отсчетов. Они отвечают вполне определенным физическим процессам, происходящим в оптико-информационных системах, в частности, в когерентных оптических системах. Ниже рассматриваются эти преобразования и их реализация в когерентной оптике.

1.3.1. Преобразование Фурье

Преобразование Фурье переводит сигнал из пространства координат в пространство частот. Это преобразование и его применение к определению частотного (временного и пространственного) спектра светового излучения и к описанию распределения амплитуды светового поля в фраунгоферовской дифракционной картине рассматривалось нами в главах 2 и 6. В общем случае в преобразованиях Фурье – любая непериодическая функция 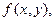удовлетворяющая некоторым условиям. В частности, она должна быть абсолютно интегрируема, т.е. интеграл по бесконечным пределам от функции , должен быть конечной величиной: ,

где x, y – координаты в обычном физическом пространстве. Фигурирующие в преобразовании Фурье переменные u и v, представляют собой координаты в обратном так называемом фурье-пространстве (пространственные частоты). Функцию f (x, y) и ее спектр F (u, v) называют парой преобразования Фурье. Ядром преобразования Фурье служит комплексная экспонента а ядром обратного преобразования – комплексная экспонента (ядром временного преобразования Фурье является функция , а временного обратного преобразования – функция ). Различие в знаках, содержащихся в экспонентах, и отличает прямое преобразование Фурье от обратного (инверсного) преобразования. В соответствии с определениями, данными выше, применение прямого, а затем обратного преобразования Фурье дает исходную функцию. Следовательно, обратное преобразование Фурье позволяет восстановить исходную функцию по ее фурье-образу. Это свойство фурье-преобразования называют его обратимостью. Как видим, в преобразовании Фурье исходная функция представляется в виде бесконечной суммы гармоник последовательно возрастающих частот. При этом фурье-образ исходной функции значительно отличается от нее самой, хотя ядра прямого и обратного преобразований отличаются только знаком перед i в показателях экспонент. Однако преобразование Фурье изображает исходную функцию однозначно, так что при повторном преобразовании Фурье исходная функция полностью восстанавливается.

Операция преобразования Фурье, связывающая координатную и частотную области, отражает физическую сущность действия оптических систем, поэтому это преобразование является наиболее широко используемым в оптике математическим аппаратом. Преобразование Фурье можно рассматривать как разложение сложной световой волны на множество плоских волн, направляющие косинусы которых соответствуют пространственным частотам волн. Оно применяется не только для описания поля при дифракции Фраунгофера, но и в когерентной оптической обработке информации и всюду, где требуется частотный анализ, фильтрация, корреляция и распознавание сигналов. При определенных условиях свойства когерентной оптической системы естественным образом описываются оператором фурье-образа, что в общем случае представляет собой двумерное преобразование Фурье.

Часто при анализе или синтезе линейных оптических систем с целью применения математического аппарата Фурье оптический сигнал рассматривают как распределение поля в плоскости XY с комплексной амплитудой, зависящей как от координат x и y, так и от времени t, т.е. считать, что сигнал имеет пространственно-временную природу. Такой сигнал (его иногда называют радиооптическим сигналом) должен описываться комплексной функцией E (x, y, t). Если использовать ту же процедуру, которая применяется к временным и пространственным сигналам, то для пространственно-временного сигнала формулу преобразования Фурье следует использовать в виде

E (u, v, n)

а обратное преобразование Фурье – в виде

E (x, y, t)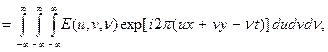

где u, v – пространственные частоты, n - временная частота. Как видим, в случае пространственно-временного сигнала речь идет о пространственно-временном частотном спектре.

Если комплексную амплитуду пространственно-временного сигнала можно представить в виде произведения двух функций E (x, y, t) = E ₁(x, y)× E ₂(t), то все операции фурье-анализа можно проводить раздельно, осуществив сначала временной фурье-анализ, а затем пространственный, или в обратной последовательности.

Не нашли, что искали? Воспользуйтесь поиском: