Преобразование Дирака и преобразование отсчетов

Соотношение

f (x, y) = f (x, y)* d (x, y) = ,

известное как фильтрующее свойство дельта-функции, называется интегральным преобразованием Дирака для свертки. Функцию можно рассматривать как «дираковский образ». В результате преобразования Дирака исходной функции получается значение исходной функции для заданного значения аргумента. Совокупность таких значений определяет исходную функцию. Как видим, дираковский образ состоит из последовательности d - функций, умноженных на значение исходной функции в соответствующих точках. Преобразование Дирака описывает идеализированную операцию сканирования или развертки сигнала вдоль координат x и y с помощью бесконечно острого луча.

В одномерном случае преобразование Дирака определяется как

f (x) = .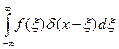

Если вместо d -функции Дирака ввести интегральное ядро вида

= a sinc(a x)× b sinc(b y), (8.8)

то получим интегральное преобразование

S (x, y) = ,

называемое преобразованием отсчетов. Это название связано с тем, что ядро вида (8.8) в оптике называют двумерной функцией отсчетов. В одномерном случае преобразование отсчетов

S (x) = ,

т.е. является сверткой функции f (x) с функцией . При a ® ¥ и b ® ¥ функция отсчетов стремится к d -функции а преобразование отсчетов переходит в преобразование Дирака, поэтому оба эти преобразования очень похожи друг на друга. Отличие преобразования отсчетов от преобразования Дирака состоит в том, что в этом преобразовании функция f (x, y) сканируется не бесконечно узким лучом, а лучом, размытым вдоль координат x и y; происходит процесс сглаживания исходной функции. При преобразовании отсчетов происходит отображение средних значений исходной функции на некотором интервале.

Преобразование отсчетов используется для обрезания или сужения спектра пространственных частот исходного сигнала f (x, y).

Преобразование отсчетов можно рассматривать как обобщение теоремы Котельникова, называемой также теоремой отсчетов. Согласно этой теореме, любую функцию f (x), имеющую ограниченный спектр пространственных частот (от u = 0 до некоторого максимального значения u = u _c), можно разложить в ряд по ортогональным функциям y (x), причем коэффициенты разложения с_m являются дискретными значениями функции f (x), взятыми через интервал D x = 1 / 2 u _c, т.е.

f (x) = , (8.9)

где c_m = f (m D x) – значения функции f (x) в точках x = m D x = m / / 2 u _c,

y_m (x) = = sinc[2 u _c(x - m D x)], | m | = 0, 1, 2, …

Для доказательства этой теоремы рассмотрим простейший одномерный сигнал с ограниченной полосой частот, у которого спектральная плотность g (u) равна постоянной величине 1 / 2 u _c в интервале частот от – u _c, до u _c и нулю вне этого интервала, т.е.

Используя обратное преобразование Фурье, находим этот сигнал:

y ₀(x) = =

= sinc(2 u _c x).

Функция y ₀(x) = sinc(2 u _c x) имеет максимальное значение, равное единице; в точках x = m / 2 u _c, | m | = 1, 2, 3, … она равна нулю. При смещении этой функции вдоль оси X на целое число интервалов D x = 1 / 2 u _c получаются функции

y_m (x) = y ₀(x - m D x) = sinc[2 u _c(x - m D x)],

ортогональные друг другу, т.е.

= 1 / 2 u _c при m = n

и 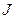= 0 при m ¹ n.

Это свойство функций y_m (x) позволяет использовать их в качестве базиса. Поэтому любую функцию f (x) со спектром, заключенным в полосе частот от 0 до u_c, можно представить в виде ряда Котельникова (8.9). Для определения коэффициентов разложения c_m положим x = n D x = n / 2 u _c, где n – целое число. Тогда получим

f (x) = = sinc(n – m).

При m ¹ n это выражение равно нулю, а при m = n – единице. Отсюда получаем c_m = f (m D x). Теорема Котельникова доказана.

Обозначим период, соответствующий наивысшей частоте u_c через l _c, т.е. положим В этих обозначениях коэффициенты разложения можно записать в виде . Таким образом, функция с ограниченным спектром полностью определяется своими значениями, взятыми через интервал D x = l _c / 2.

Используя условие ортогональности, из (8.9) можно получить выражение для энергии сигнала:

.

Хотя суммирование в ряде Котельникова ведется в бесконечных пределах, в действительности число значений функции f (x) ограничено и определяется длиной сигнала L и шириной его полосы частот u_c:

N = L / D x = 2 L / l_c = 2 Lu _c.

При N >> 1 погрешность от перехода к конечному пределу суммирования невелика, т.е. в интервале 0 £ x £ L функция f (x) полностью определяется N выборками из нее. От числа N зависит количество информации, содержащееся в данном сигнале f (x) (точнее от N + 1, так как число точек на единицу больше числа интервалов). В оптике в качестве периода l _c принимают размер наиболее мелкой детали l_min, а в качестве длины сигнала L – длину транспаранта.

Для двумерного сигнала f (x, y) ряд Котельникова имеет вид

f (x, y) = 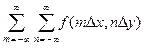sinc[2 u _c(x - m D x)]∙

∙ sinc[2 v _c(y - n D y)],

где u _c и v _c – граничные частоты по соответствующим переменным x и y.

Теорема Котельникова имеет важное значение в теории сигналов и в оптике. На ее основе любой непрерывный сигнал может быть со сколь угодно высокой степенью точности преобразован в дискретный.

Не нашли, что искали? Воспользуйтесь поиском: