
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятие линейной оптической системы
Оптической системой называют прозрачные изотропные тела, преломляющие и отражающие световые лучи. Оптическая система представляет собой набор последовательно расположенных друг за другом оптических элементов. Такими оптическими элементами являются слой свободного пространства, диафрагмы (отверстия в непрозрачном экране), линзы, плоские пластинки, призмы, решетки и т.д. В дальнейшем будут рассматриваться центрированные относительно оси Z оптические системы. Оптические элементы системы (за исключением слоя свободного пространства) будут представляться в виде тонкого экрана, модулирующего световой поток, проходящий через него в каждой точке экрана. Элементарный световой сигнал будет рассматриваться как луч света, проходящий в данной точке экрана. Необходимым условием применимости такого представления является выполнение неравенства h << d 2 / l, где h – толщина экрана, d – пространственный период сигнала. При этом условии луч света проходит экран, не расширяясь (зона Френеля).
Оптическая система называется линейной, если ее реакция (или отклик) на сумму элементарных воздействий, называемую входным сигналом, равна сумме реакций на каждое элементарное воздействие, представляющей световой сигнал. Понятие линейной системы, как уже отмечалось, пришло в оптику из радиотехники и теории связи. Оказывается, что оптические системы и рассматриваемые в теории электрических цепей линейные четырехполюсники сходны между собой. Например, линзу можно и удобно представить в виде четырехполюсника. Подобно четырехполюснику оптическую систему, создающую изображение, можно рассматривать как систему, преобразующую сигналы. Поведение такой системы, как и поведение четырехполюсника, описывается соотношением между возбуждением на входе и реакцией на выходе.
Рассматриваемые в радиотехнике сигналы представляют собой функции времени, т.е. зависят от одной переменной – времени t. В оптике сигналом называют пространственное распределение амплитуды (при использовании когерентного света) или интенсивности (при некогерентном освещении) светового поля, т.е. функции E (x, y) или I (x, y) в некоторой плоскости XY. Оптические сигналы обычно записываются на фотопленках или фотопластинках, которые в данном случае называются транспарантами (диапозитивами). Коэффициент пропускания транспаранта t (x, y) по амплитуде пропорционален зарегистрированному сигналу E (x, y). Этот коэффициент, как известно, связывает между собой комплексную амплитуду светового поля на входе оптической системы с комплексной амплитудой поля на выходе. При восстановлении сигнала транспарант освещают плоской или сферической волной. Распределение поля в плоскости непосредственно за предметом (транспарантом) называется входным (для оптической системы) сигналом, а саму плоскость, расположенную непосредственно за предметом, – плоскостью предмета или входной плоскостью (иногда эту плоскость называют пространством входного сигнала). Функция пропускания предмета в общем случае является комплексной: t (x, y) = | t (x, y)| e i j ( x , y ), причем модуль этой функции характеризует прозрачность предмета, а ее аргумент – набег фазы световой волны в предмете, зависящий от его толщины. В соответствии с этим предмет преобразует поле падающей на него световой волны по закону
E (x, y) = E 0(x, y) t (x, y) = E 0(x, y) | t (x, y)| e i j (x, y),
т.е. пространственно модулирует это поле по амплитуде и фазе (или только по одной из этих характеристик). Амплитудная модуляция определяется модулем функции пропускания | t (x, y)|, а фазовая – его аргументом j (x, y). Промодулированная предметом световая волна, распространяется вдоль оси Z и, пройдя сквозь оптическую систему, образует в некоторой плоскости X¢Y¢ распределение амплитуды E (x¢, y¢) (или интенсивности 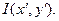 Распределение, получившееся в плоскости X¢Y¢ после преобразования оптической системой распределения E (x, y) (или I (x, y)), называют выходным сигналом или реакцией оптической системы на входной сигнал, а плоскость X¢Y¢ – выходной плоскостью или плоскостью изображения (иногда пространством выходного сигнала). Характеристики выходного сигнала определяются, таким образом, как характеристиками входного сигнала, так и характеристиками оптической системы.
Распределение, получившееся в плоскости X¢Y¢ после преобразования оптической системой распределения E (x, y) (или I (x, y)), называют выходным сигналом или реакцией оптической системы на входной сигнал, а плоскость X¢Y¢ – выходной плоскостью или плоскостью изображения (иногда пространством выходного сигнала). Характеристики выходного сигнала определяются, таким образом, как характеристиками входного сигнала, так и характеристиками оптической системы.
Рассмотрим необходимые условия линейности оптической системы. Обозначим исходный (входной) сигнал через f (x, y), а конечный (выходной) сигнал – через F (x´, y´), где x, y – координаты во входной, а x´, y´ – в выходной плоскостях (предмета и изображения). По аналогии с радиотехникой входной сигнал часто называют возбуждением, а выходной сигнал – откликом или реакцией на входное воздействие. Предположим, что входной сигнал f 1(x, y) дает на выходе реакцию F 1(x´, y´), а сигнал f 2(x, y) – реакцию F 2(x¢, y¢). Если оптическая система является линейной, то возбуждение на входе f 1(x, y) + f 2(x, y) вызывает реакцию F 1(x¢, y¢) + F 2(x¢, y¢) на выходе. Таким образом, необходимым условием линейности оптической системы является выполнение принципа суперпозиции, согласно которому если на систему действует несколько сигналов, то каждый один сигнал не влияет на реакцию, вызванную другим сигналом, и выходной сигнал от суммы входных сигналов равен сумме сигналов от каждого входного сигнала, действующего поодиночке. Следовательно, в основе деления систем на линейные и нелинейные лежит условие применимости принципа суперпозиции, сформулированное относительно операции суммирования сигналов на выходе системы. Пусть, далее, cf (x, y) – сигнал на входе оптической системы, где c – произвольная постоянная. Тогда для линейной оптической системы этому возбуждению на входе будет соответствовать реакция cF (x, y) на выходе. Это второе необходимое условие линейности оптической системы описывает свойство гомогенности системы. Оно выражает собой свойство сохранения масштаба линейной системой. Следовательно, оптическая система линейна тогда и только тогда, когда она обладает свойствами аддитивности и гомогенности.
Выходной сигнал является результатом действия оптической системы на входной сигнал. Это действие можно выразить мате-
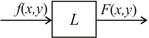 Рис. 1.1
Рис. 1.1
|
матически как действие некоторого оператора L, присущего данной оптической системе. Оператор показывает, как нужно подействовать на входную функцию 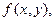 чтобы получить выходную функцию
чтобы получить выходную функцию 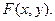 Введя понятие оператора, преобразование входного сигнала в выходной сигнал можно записать в символической форме
Введя понятие оператора, преобразование входного сигнала в выходной сигнал можно записать в символической форме
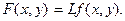
Действие оператора L показано на рис. 1.1. Линейная оптическая система описывается линейным оператором L. Оптическая система является линейной, если, например, для двух входных сигналов f 1(x, y) и f 2(x, y) и для двух постоянных c 1 и c 2 входной сигнал c 1 f 1 (x, y) + c 2 f 2 (x, y) преобразуется в выходной сигнал c 1 F 1(x, y) + c 2 F 2 (x, y), т.е. если
L { c 1 f 1(x, y) + c 2 f 2(x, y)} = c 1 F 1(x, y) + c 2 F 2 (x, y).
Для произвольного числа n воздействий это условие можно записать в виде:
 =
= 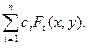 . (1.1)
. (1.1)
Соотношение (1.1) описывает одновременно и свойство аддитивности и свойство гомогенности линейной оптической системы.
Среди всех линейных оптических систем наибольшее значение в фурье-оптике имеют пространственно-инвариантные (инвариантные относительно сдвигов в координатной области) и частотно-инвариантные (инвариантные относительно сдвигов в частотной области) оптические системы. Первые называются фильтрами, а вторые – модуляторами. Фильтром является, например, слой свободного пространства, заключенный между двумя параллельными плоскостями. К модуляторам относятся апертуры, дифракционные решетки, зеркала, призмы, линзы.
Для линейных пространственно-инвариантных оптических систем имеет место соотношение
F (x – x 0; y – y 0) = L { f (x – x 0; y – y 0)}.
Это означает, что если входное воздействие f (x, y) вызывает выходную реакцию F (x, y), то входное воздействие f (x – x 0; y – y 0) вызывает реакцию F (x – x 0; y – y 0). Здесь x 0 и y 0 – постоянные; масштаб системы координат в плоскости XY выбран так, что коэффициент увеличения равен единице.
Частотная инвариантность означает, что если спектральные плотности входного и выходного сигналов соответственно g (u, v) и G (u, v), то при спектральной плотности входного сигнала g (u – – u 0; v – v 0) спектральная плотность выходного сигнала будет G (u – u 0; v– v 0), где u 0 и v 0 – постоянные. В операторном виде это утверждение можно записать так:
G (u – u 0; v – v 0) = L { g (u – u 0; v – v 0)}.
Пространственно-инвариантные линейные оптические системы (фильтры) обладают важным свойством: они не создают новых пространственных частот. Это означает, что если входное воздействие f (x, y), приложенное к такой системе, содержит в своем спектре пространственные частоты u и v, то и вызываемая им выходная реакция F (x, y) будет содержать те же самые частоты u и v.
Фильтры можно характеризовать импульсной характеристикой h (x, y) и передаточной функцией H (u, v), так как эти величины не зависят от сдвигов в координатной области. (Термины «импульсный отклик», «импульсная характеристика» и «передаточная функция» так же, как и термин «линейная система», пришли в фурье-оптику из теории связи).
Модуляторы характеризуются функцией пропускания t (x, y). Эта величина не зависит от сдвигов в частотной области. Убедимся в этом. Запишем обратное фурье-преобразование функции f (x, y) в предположении, что ее пространственно-частотный спектр смещен на величины u 0, v 0. Обозначив через f 1(x, y) функцию, описывающую входной сигнал со смещенным спектром, будем иметь
f 1(x, y) = 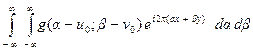 =
=
=  =
=
=  =
=
= f (x, y) exp[ i 2 p (u 0 x + v 0 y)].
Аналогично можно получить и для выходного сигнала:
F 1(x, y) = F (x, y) exp[ i 2 p (u 0 x + v 0 y)]. 
С учетом этого для функции пропускания получим
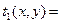
 .
.

Отсюда видно, что, хотя при сдвиге частот входной и выходной сигналы приобретают фазовый множитель exp[ i 2 p (u 0 x + v 0 y)], функция пропускания модулятора, определяемая отношением этих сигналов, от сдвигов в частотной области не зависит (не зависит от u 0, v 0).
Понятия импульсной характеристики и передаточной функции рассматриваются в п.п. 9.1 и 9.2.
Не нашли, что искали? Воспользуйтесь поиском: