Преобразование Гильберта

Прямое преобразование Гильберта определяется соотношением

g (x) ,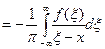

а обратное преобразование – соотношением

f (x) .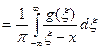

Заметим, что в отличие от других функций и их преобразований, которые определяются в сопряженных областях, в преобразовании Гильберта функции g и f являются функциями одной переменной x. Между этими функциями существует несимметрично-обратное соотношение (обратное, если исключить знак минус). Говорят, что функции g (x) и f (x) сопряжены друг другу. Функцию g (x) иногда называют функцией квадратуры, соответствующей функции f (x).

Видим, что прямое и обратное преобразования Гильберта представляют собой операции свертки соответственно с функциями –1/ px и 1/ px. Это приводит к особенно простому соотношению между g (x) и f (x) в пространстве координат преобразования Фурье.

Преобразование Гильберта связывает действительную и мнимую части аналитического сигнала. Для функции одной пространственной координаты аналитический сигнал можно определить в виде

z (x) = 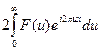= f (x) + i g (x),

где g (x) и определяется преобразованием Гильберта функции f (x). При этом если, например, f (x) = 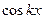, то g (x) = 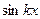, если f (x) = 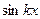, то g (x) = – 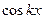. Аналитический сигнал по одной из координат для объектов, характеризующихся комплексно-симметричной функцией пропускания, можно получить в оптической системе, показанной на рис. 8.4. На вход системы поступает сигнал 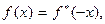половина которого перекрывается оптическим ножом. Действие ножа описывается ступенчатой функцией Хевисайда 1(x), т.е. распределение поля в плоскости пространственных частот (фокальной плоскости линзы) имеет вид R (u) = F (u)×1(u), где

1(u) = F{1(x)} =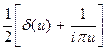

– фурье-образ ступенчатой функции Хевисайда (формула (3.)). При этом фурье-образ функции z (x)

Z (u) = F{ z (x)} ~ R (u).

Используя дальнейшее преобразование Фурье, получим непосредственно аналитический сигнал z (x).

В оптических системах формирования изображения аналитический сигнал можно получить, перекрыв маской половину выходного зрачка.

Рассмотрим оптическое преобразование Гильберта. Для этого найдем фурье-образ аналитического сигнала:

Z (u) = F (u) + iG (u) = 2 F (u)1(u) = 2 F (u) при u > 0

и Z (u) = 0 при u < 0,

Отсюда и получаем упомянутое выше простое соотношение между фурье-образами функций g (x) и f (x):

G (u) = - i [2 F (u)1(u) – F (u)] = - iF (u)×sign(u) = – iF (u) при u > 0

и G (u) = iF (u) при u < 0,

где функция знака sign(s) принимает значение, равное +1 при s > > 0 и равное –1 при s < 0.

Из полученного соотношения видно, что преобразование Гильберта осуществляется в линейной системе с передаточной функцией H (u) = - i sign(u) = - i = 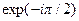при u > 0 и H (u) = i = 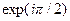при u < 0.

Оптическая схема, по которой осуществляется такое преобразование, показана на рис. 8.5 На схеме первая линза L ₁ формирует пространственный спектр сигнала f (x) в плоскости u. Здесь установлен фазовый фильтр (p -фазовая ступенька), которая изменяет фазу отрицательных компонент на p. На выходе системы наблюдается сигнал g (x), соответствующий преобразованию Гильберта функции f (x). Схема преобразования Гильберта двумерных сигналов отличается от вышеприведенной схемы только тем, что на вход первой линзы L ₁ подается двумерный сигнал и тем что в плоскости пространственных частот u, v устанавливается фазовая пластинка, которая вносит сдвиг фазы на p в четных или нечетных квадрантах. На выходе такой системы формируется сигнал g (x, y), соответствующий двумерному преобразованию Гильберта.

Преобразование Гильберта используется для уменьшения диапазона пространственных частот системы формирования изображения, сохранив при этом разрешение конечной картины. Такая задача может возникнуть при передаче сигнала по каналу с ограниченной пропускаемой способностью.

Не нашли, что искали? Воспользуйтесь поиском: