Импульсная характеристика и передаточная функция слоя свободного пространства

Простейшей линейной пространственно-инвариантной оптической системой, преобразующей входной сигнал E (x, y) в выходной сигнал является слой свободного пространства, заключенный между двумя параллельными плоскостями XY и X¢Y¢. Обычно в этих плоскостях размещаются различные оптические элементы (линзы, диафрагмы, транспаранты и т.п.). Так как слой пространства является фильтром, то его свойства описываются импульсной характеристикой и передаточной функцией. Найдем эти характеристики.

Пусть в координатной плоскости XY задано распределение поля E (x, y). Тогда распределение поля = в плоскости X¢Y¢, находящейся на расстоянии z от входной плоскости, найдется с помощью интеграла Кирхгофа – Френеля – Зоммерфельда (5.3). Представим амплитудный весовой множитель в виде Тогда с учетом (5.4) для поля будем иметь

(9.14)

Полученный интеграл представляет собой интеграл свертки входного сигнала E (x, y) с функцией

h (x, y) = . (9.15)

Эта функция и является импульсной характеристикой слоя свободного пространства толщиной z. Следовательно, интеграл суперпозиции Кирхгофа – Френеля – Зоммерфельда можно записать в виде

E¢ (x¢, y¢) =

Это соотношение показывает, что распространение оптического сигнала в свободном пространстве описывается линейным преобразованием или, другими словами, распространение световой волны в однородной среде можно рассматривать как преобразование сигнала в линейной пассивной системе. Это соотношение показывает также, что поле в плоскости X¢Y¢ определяется сверткой поля в плоскости XY с импульсной характеристикой слоя свободного пространства.

Физический смысл полученной импульсной характеристики состоит в том, что точечный источник света, расположенный в начале координат (x = 0, y = 0), создает сферическую волну, которая в плоскости X¢Y¢ вызывает изменение фазы сигнала по гиперболическому закону при медленном уменьшении амплитуды с увеличением расстояния от оси Z. Как и следовало ожидать, импульсная характеристика симметрична относительно оси Z.

Для определения передаточной функции свободного пространства, в соответствии с (9.8), следует найти фурье-образ функции (9.15):

H (u, v) =

= .

Вычисление этого интеграла методом стационарной фазы дает следующее простое выражение для передаточной функции свободного пространства:

H (u, v) = , (9.16)

где учтено, что волновое число k = 2 p / l.

К выражению (9.16) для передаточной характеристики свободного пространства можно придти и иначе. Во входной плоскости XY поле характеризуется частотным спектром E (u, v) (или E (u, v; 0)), в выходной плоскости X¢Y¢ – спектром E¢ (u, v) (или E (u, v; z), где координату z можно рассматривать в качестве параметра). В результате распространения поля на расстояние z (от входной плоскости XY до выходной плоскости его фурье-спектр претерпевает изменение по фазе, определяемое экспоненциальным множителем . Таким образом,

E¢ (u, v) = E (u, v) .

Учитывая соотношение (9.11), приходим к выражению (9.16).

Заметим, что, в соответствии с этим выражением, распространение волн в свободном пространстве на расстояние z проявляется только в изменении относительных фаз различных составляющих углового спектра. Фазовые сдвиги возникают вследствие того, что плоские волны, распространяясь под различными углами, проходят различные расстояния, пока достигнут рассматриваемой точки.

Представляет интерес также получить выражение (9.16) и из решения волнового уравнения Гельмгольца для свободного пространства с помощью двумерного преобразования Фурье. Умножим волновое уравнение Гельмгольца

на выражение и проинтегрируем по x и y в бесконечных пределах. Вычисление первых двух интегралов дает соответственно выражения – u ² E (u, v; z) и – v ² E (u, v; z). Третье слагаемое приводится к виду , а четвертое – к виду С учетом этого приходим к уравнению

.

Решением этого обыкновенного дифференциального уравнения второго порядка является функция вида

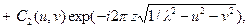
где C ₁ и C ₂ – постоянные интегрирования (они не зависят от координаты z, но могут зависеть от пространственных частот u и v). Первый член в этом выражении соответствует прямой волне, а второй – обратной. В свободном пространстве обратная волна отсутствует, поэтому второй член должен быть равен нулю. Учитывая далее, что в плоскости z = 0 пространственный спектр распределения поля есть E (u, v; 0), найдем, что C ₁(u, v) = E (u, v; 0). Тогда получим

.

Следовательно, для определения спектра выходного сигнала E (u, v; z) нужно спектр входного сигнала E (u, v; 0) умножить на функцию частот u и v:

,

которой и является передаточная функция свободного пространства.

Заметим, что передаточная функция слоя свободного пространства представляет собой фазовый множитель в выражении плоской волны.

Выражение (9.16) показывает, что слой свободного пространства играет роль оптической системы, фильтрующей пространственные частоты. Область пропускания этого фильтра определяется условием

(9.17)

В плоскости пространственных частот это соотношение определяет круг радиуса . Соотношение (9.17) представляет собой условие распространения световых волн с частотами u и v. Если это условие не выполняется, квадратный корень в экспоненте (9.16) становится мнимым, а сама экспонента – действительной величиной с отрицательным показателем степени. Это приводит к появлению в амплитуде плоской волны (1.30) экспоненциально убывающего множителя где

.

Такие волны (их называют неоднородными или поверхностными волнами) могут распространяться вдоль плоскости XY и быстро затухают (практически на расстоянии нескольких длин волн l) при удалении от этой плоскости (с ростом z). Передаточная функция H (u, v) при z >> l и невыполнении условия (9.17) близка к нулю. Поэтому пропускание свободного пространства вне круга радиуса близко к нулю. Отсюда следует, что волны, частоты u и v которых не удовлетворяют условию (9.17), на расстоянии z >> l от входной плоскости не содержат никакой информации о пространственных частотах оптического поля E (x, y). Чем больше длина участка свободного пространства z, тем меньше сквозь него проходит пространственных частот.

Поскольку частотная характеристика слоя свободного пространства является величиной комплексной, она может быть представлена в виде

H (u, v) = | H (u, v)| exp[ ij (u, v)].

При этом модуль этой функции | H (u, v)| определяет амплитудно-частотную, а аргумент

– фазо-частотную характеристики слоя свободного пространства. Внутри круга АЧХ

| H (u, v)| = 1,

а ФЧХ

,

а вне этого круга АЧХ

,

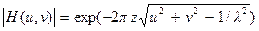ФЧХ

В приближении Френеля, когда импульсную характеристику свободного пространства можно получить, учтя, что в приближении Френеля z + , и положив в знаменателе предэкспоненциального множителя в (9.15) Будем иметь

h (x, y) = =

= . (9.18)

Это соотношение можно записать и в такой форме:

(9.19)

где коэффициент не зависит от координат x и y.

Как видим, фаза импульсной характеристики слоя свободного пространства изменяется по квадратичному закону относительно переменных x и y, а ее амплитуда уменьшается обратно пропорционально толщине слоя z. От координат x и y амплитуда импульсной характеристики слоя свободного пространства не зависит. Заметим, что импульсная характеристика слоя свободного пространства представляет собой расходящуюся сферическую волну с радиусом кривизны, равным толщине слоя z. Отметим также, что свойства слоя свободного пространства определяются только одним параметром – его глубиной z.

Передаточную функцию слоя свободного пространства в приближении Френеля найдем, подставив (9.18) в (9.8):

=

=

или

(9.20)

где – коэффициент, не зависящий от переменных u и v. При получении конечного выражения мы воспользовались значением интеграла

(9.21)

при a = p / (ilz), b ₁ = i 2 pu, b ₂ = i 2 pv.

Выражение (9.19) для H (u, v) в приближении Френеля можно получить и непосредственно из общего выражения (9.16), полагая, что в этом приближении

.

Первый экспоненциальный множитель в передаточной функции (9.20) описывает общее изменение фазы для каждой компоненты спектра, обусловленное прохождением ее от входной плоскости до выходной плоскости, расстояние между которыми равно z. Этот множитель – постоянный в плоскости XY, поэтому в выражениях (9.18) и (9.19) его можно опустить. Второй экспоненциальный множитель описывает фазовую зависимость волны от пространственных частот (фазовую дисперсию) по квадратичному (параболическому) закону. Как видим, в приближении Френеля для всех частот амплитудно-частотная характеристика слоя свободного пространства | H (u, v)| постоянна и равна единице, а его фазо-частотная характеристика 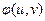изменяется по закону

Частотную характеристику слоя свободного пространства можно также представить в виде

(9.22)

с тем же коэффициентом не зависящим от частот u и v. Заметим, что обе характеристики слоя свободного пространства – импульсная и частотная определяются только одним параметром – его толщиной z.

Глава 4

Не нашли, что искали? Воспользуйтесь поиском: