Линейность оптической системы при различных видах освещения

Пусть в оптической системе, освещаемой когерентным светом, входным комплексным амплитудам и соответствуют выходные комплексные амплитуды 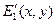и . Если система линейна, то комплексной амплитуде E ₁(x, y) + + E ₂ на входе должна соответствовать комплексная амплитуда на выходе. Выходная интенсивность будет при этом иметь вид многочлена:

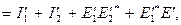(9.28)

где – выходная интенсивность при действии на входе только сигнала E ₁, а – выходная интенсивность при действии только сигнала E ₂. При когерентном освещении все четыре члена в (9.28), вообще говоря, не равны нулю. Следовательно, в этом случае система не линейна по интенсивности. Однако при некогерентном освещении выходная интенсивность складывается только из выходных интенсивностей: , т.е. системы, освещаемые некогерентным светом, линейны по интенсивности.

Различие между этими случаями является фундаментальным и составляет основу обсуждения процесса образования изображения, рассматриваемого в главах 11 и 12.

Рис. 9.3

Рассмотрим теперь оптическую систему (рис. 9.3), состоящую из протяженного источника света S, транспаранта T, расположенного в плоскости XY, оптической системы формирования изображения (на рисунке показана в виде прямоугольного параллелепипеда с входным и выходным отверстиями) и выходной плоскости (плоскости изображения) X¢Y¢. Разобьем мысленно источник света на элементарные излучатели площадью ds. Пусть – комплексная амплитуда поля в плоскости непосредственно перед транспарантом, обусловленного элементарными источниками света. Если функция пропускания транспаранта по амплитуде 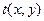, то комплексное световое поле в плоскости непосредственно за транспарантом будет E (x, y) = E ₀(x, y) t (x, y). Предположим, что оптическая система линейна, пространственно-инвариантна и имеет пространственную импульсную характеристику Тогда комплексное световое поле в выходной плоскости X¢Y¢, обусловленное элементарным источником, можно описать уравнением свертки

E¢ (x¢, y¢) = E (x, y)* h (x, y; x¢, y¢) = E ₀(x, y) t (x, y)

h (x, y; x¢, y¢). (9.29)

Интенсивность в выходной плоскости от элементарного источника света

dI′ (9.30)

а полная интенсивность в выходной плоскости, создаваемая всем источником света, будет

I′ = , (9.31)

где интегрирование проводится по всей площади s источника света S. Выражение (9.31) можно записать в виде интеграла свертки

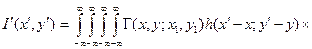
, (9.32)

где

Г(x, y; x ₁, y ₁) =

представляет собой функцию взаимной пространственной когерентности. Эта функция характеризует статистическую связь полей в плоскости предмета. В параксиальном приближении функция определяется соотношением (4.25).

Г(x, y) ,

где I_S (x, h) – интенсивность источника света, приходящаяся на единицу площади его поверхности на единичном расстоянии от него, 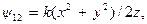x, h – координаты в плоскости источника света.

Рассмотрим два предельных случая.

1. Источник света пренебрежимо мал, т.е. I_S (x, h) = d (x, h). В этом случае

Г(x, y) = C ₁, (9.33)

где C ₁ – положительная постоянная. Функция взаимной пространственной когерентности Г отлична от нуля для любой пары точек в плоскости предмета. Этот случай соответствует полностью пространственно когерентному освещению (или, как говорят, полностью когерентной оптической системе), так как в этом случае имеет место статистическая связь между полями в плоскости предмета. Такое освещение можно получить от точечного источника света, расположенного в фокусе собирающей линзы без аберраций, поставленной перед транспарантом. С этой целью можно использовать и пучок лазерного излучения, который, как известно, обладает хорошей пространственной когерентностью даже при искусственном расширении пучка. В этом случае транспарант освещается коллимированным пучком света, т.е. плоской волной. Распределение поля в плоскости непосредственно за транспарантом будет пропорционально его функции пропускания по амплитуде t (x, y). При полностью когерентном освещении

I′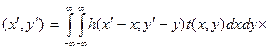

=

= E¢ (x¢, y¢)× E¢ ^*(x¢, y¢). (9.34)

Отсюда получаем

E¢ (x¢, y¢) = , (9.35)

где E (x, y) пропорционально t (x, y) – распределение комплексной амплитуды в предметной плоскости. Следовательно, в случае полностью когерентного освещения оптическая система линейна по комплексной амплитуде. При этом комплексная амплитуда на выходе определяется сверткой комплексной амплитуды на входе с импульсной характеристикой системы.

2. Источник света бесконечно большой, а его излучение однородно, т.е. I_S (x, h) = const. В этом случае функция взаимной пространственной когерентности

Г(x, y) = C ₂ d (x, y), (9.36)

где C ₂ – комплексная постоянная. Это означает отсутствие статистической связи между полями точечных источников в плоскости предмета. Значение функции Г(x, y) отлично от нуля лишь в точках (x, y), поэтому выражение (9.36) соответствует полностью некогерентному освещению (описывает полностью некогерентную оптическую систему формирования изображения). Такое освещение можно получить от протяженного источника с помощью подходящего коллиматорного устройства. Следовательно, в случае полностью некогерентного освещения распределение интенсивности в выходной плоскости записывается в виде

I′

или

I′ 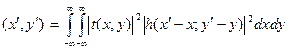. (9.37)

Стоящая в подынтегральном выражении (9.37) функция называется функцией пропускания транспаранта по интенсивности. Она будет пропорциональна распределению интенсивности поля в предметной плоскости I (x, y). С учетом этого интеграл (9.37) можно переписать в виде

или

I′ 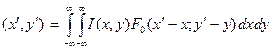. (9.38)

Здесь 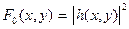. Функцию называют импульсной характеристикой оптической системы по интенсивности, некогерентной переходной функцией оптической системы, а также функцией рассеяния точки (сокращенно ФРТ). Эта функция описывает распределение интенсивности в изображении светящейся точки. Поскольку представляет интерес лишь относительное распределение интенсивности I, оказывается удобным нормировать ФРТ на единицу, т.е. положить

. (9.39)

Таким образом, в случае полностью некогерентного освещения интенсивность поля в выходной плоскости представляет собой свертку интенсивности входного сигнала с импульсной характеристикой системы по интенсивности. В случае полностью некогерентного освещения оптическая система является линейной относительно интенсивности.

В отличие от когерентного сигнала некогерентный сигнал 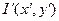описывается не комплексной, а действительной функцией. Эта функция несет информацию, заложенную в интенсивности световой волны. Следовательно, некогерентный сигнал несет только амплитудную информацию; фазовая информация утрачивается.

Таким образом, полностью когерентная оптическая система является линейной по амплитуде, а полностью некогерентная – по интенсивности. Общее выражение (9.32) соответствует частично-когерентному освещению.

Используя коммутативное свойство свертки, получим другое, более удобное, выражение для интенсивности поля в выходной плоскости:

. (9.40)

Не нашли, что искали? Воспользуйтесь поиском: