Фазовое преобразование тонкой линзы

В тонкой линзе поглощением света, а значит, изменением амплитуды проходящей световой волны можно пренебречь (отражением света от поверхности линзы также пренебрегаем). Тонкая линза просто задерживает фронт падающей волны на величину, пропорциональную толщине линзы. Она изменяет только фазу проходящей через нее волны. В этом смысле тонкая линза является фазовым экраном – устройством, изменяющим фазу падающего на него волны, подобным, например, зонной пластинке Вуда. Но если зонная пластинка Вуда изменяет фазу от соседних зон Френеля на π, изменение фазы, вносимое линзой, как будет показано ниже, является непрерывным.

Получим закон изменения фазы волны, прошедшей через тонкую двояковыпуклую линзу. Поместим в центре O линзы

начало правой прямоугольной системы координат, направив ось Z вдоль оптической оси. Если линза идеальная, то точка S пространства предметов изображается в виде точки S¢ пространства изображений. Будем считать для простоты, что точка S лежит на опти-

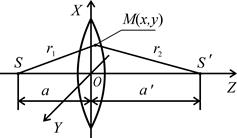Рис. 7.10

ческой оси положительной линзы на расстоянии a от нее; тогда точка изображения S¢ тоже будет лежать на оптической оси, но на расстоянии а′ от линзы (рис. 7.10). Предположим, что из точки S в точку S¢ приходят два различных световых луча: один направлен вдоль оптической оси линзы, а другой проходит через точку Согласно принципу Ферма, длины оптических путей этих лучей должны быть одинаковыми. Так как их геометрические пути различны, выравнивание оптических путей происходит в линзе. Разность геометрических путей должна быть скомпенсирована фазовым сдвигом, обусловленным линзой. Геометрический путь луча, идущего через центр линзы равен L ₁ = a + а′. Геометрический же путь луча, проходящего через произвольную точку 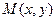линзы, находящуюся на расстоянии 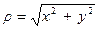от оптической оси, будет

L ₂ = r ₁ + r ₂ = + .

В параболическом приближении

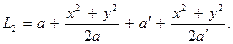
Разность геометрических путей

D = L ₂ – L ₁ @ .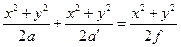

При получении этого выражения была использована формула линзы 1 / a + 1 / а′ = 1 / f. Вследствие этой разности хода волны, идущие по второму (более длинному) пути, будут отставать по фазе от волн, идущих по первому пути на величину

.

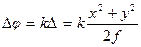Это отставание по фазе может быть скомпенсировано фазовым сдвигом , вносимым линзой. Следовательно, фазовая характеристика линзы должна иметь вид

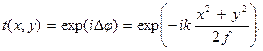(10.29)

Знак минус перед показателем степени экспоненты показывает, что волны, идущие через точку M (x, y), опережают по фазе волны, идущие через центр линзы, поэтому эти разности фаз компенсируют друг друга.

Формула (10.29) описывает пространственное преобразование фазы, осуществляемое тонкой линзой. Поэтому если поле непосредственно перед линзой E (x, y), а поле непосредственно за линзой E¢ (x, y), то можно записать

E¢ (x, y) = E (x, y) . (10.30)

Функция t (x, y) представляет собой функцию пропускания тонкой линзы. Она является важной характеристикой линзы и играет большую роль при теоретическом рассмотрении применения линзы для формирования оптического изображения и для фурье-преобразования. Видим, что действие тонкой линзы на поле проходящей световой волны сводится к умножению функции распределения этого поля в плоскости XY непосредственно перед линзой на функцию пропускания линзы.

Тем самым мы показали, что действие тонкой линзы на падающую на нее световую волну можно рассматривать как действие экрана, изменяющего фазу волны в соответствии с законом (10.29).

К формуле (10.29) можно прийти с помощью следующих простых рассуждений. Сферическая волна расходящаяся из переднего фокуса (из точки F на расстоянии f от линзы, после прохождения через линзу становится плоской. Следовательно, если формулу сферической волны с амплитудой умножить на фазовую характеристику линзы, получим плоскую волну той же амплитуды, т.е. должно выполняться равенство

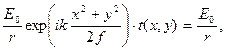
откуда получаем формулу (10.29).

Значение фазового преобразования, осуществляемого линзой, можно продемонстрировать на примере плоской волны, падающей на выпуклую линзу параллельно оптической оси (оси Z). Покажем, что после прохождения через линзу плоская волна превращается в сферическую волну, сходящуюся в фокусе линзы. Пусть комплексная амплитуда плоской волны равна E ₀. Тогда поле волны, прошедшей через линзу (в плоскости непосредственно за линзой, т.е. при z = 0), найдется умножением комплексной амплитуды E ₀ на функцию пропускания линзы t (x, y):

E (x, y, 0) = E ₀ exp .

Это соотношение описывает в параксиальном приближении поле сферической волны, сходящейся в точку, расположенную на оптической оси линзы (оси Z) на расстоянии f от начала координат, т.е. в заднем фокусе линзы F¢. Мы видим, что параллельный пучок света, распространяющийся вдоль оптической оси, после преломления в линзе сходится в ее фокусе. Плоская волна, не обладающая кривизной, после прохождения через линзу приобретает кривизну, равную 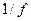и становится сферической – сходящейся при положительной кривизне или расходящейся при отрицательной кривизне.

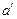Покажем также, что сферическая волна, расходящаяся из точки находящейся на расстоянии a от линзы, после прохождения через линзу сходится в точке на расстоянии от нее. Используя формулу (1.24) без учета не влияющих на распределение поля коэффициентов, получим

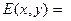exp =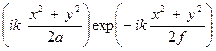

=

Используя формулу линзы (10.25), будем иметь

.

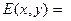exp .

Это выражение описывает сферическую волну, сходящуюся в точке находящейся на расстоянии 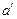от линзы.

Аналогично можно показать, что для вогнутой линзы фазовое преобразование в пренебрежении несущественной комплексной постоянной равно

t (x, y) = exp . (10.31)

Заметим, что существенная разница в фазовых преобразованиях выпуклой и вогнутой линз выражается в положительном и отрицательном знаке квадратичной фазовой задержки. Функция (10.29) описывает линзу с положительным фокусным расстоянием 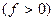, а функция (10.31) – с отрицательным фокусным расстоянием

Таким образом, линза осуществляет квадратичную фазовую модуляцию сигнала. Она сдвигает фазу падающего пучка на величину, пропорциональную квадрату расстояния между осью и точкой падения. Квадратичное фазовое преобразование, производимое линзой, является приближением сферического волнового фронта. При этом собирающая (положительная) линза создает отрицательный сдвиг фаз, а рассеивающая (отрицательная) – положительный.

Конечные поперечные размеры линзы учитываются введением в функцию пропускания в качестве множителя так называемой зрачковой функции P (x, y), определяемой как

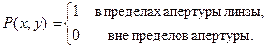
Под апертурой линзы понимают угол раскрытия пучка лучей, идущих из какой-либо точки S через линзу (или угол, под которым видно входное отверстие линзы из точки S). Иногда апертурой линзы называют область значений координат x и y, внутри которой P (x, y) ¹ 0, т.е. внутри круга 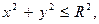где R – радиус апертуры линзы. С учетом конечных размеров линзы соотношение (11.) перепишется в виде

E¢ (x, y) = E (x, y) P (x, y) 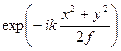. (11.32)

Собирающую линзу можно рассматривать как предельный случай фазовой зонной пластинки Вуда. Действительно, как и зонная пластинка Вуда, линза создает интерференционный максимум, изменяя фазу вторичных источников. Однако в отличие от указанной зонной пластинки, изменяющей фазу вторичных источников скачком на величину, равную π, линза обеспечивает непрерывное изменение фазы этих источников, что достигается непрерывным изменением толщины линзы, в результате чего чем ближе источник находится к оптической оси линзы, тем больше «задержка», обусловленная замедлением света в материале линзы. Вследствие этого колебания, обусловленные действием всех вторичных источников, оказываются строго синфазными только в одной точке (в случае падения на линзу плоской волны – в фокусе линзы). В этой точке (точнее, в области размером порядка длины волны λ) возникает весьма острый интерференционный максимум. Условием максимума является равенство оптических путей всех лучей, идущих через линзу в точку F¢ (или точку S¢).

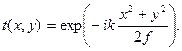(10.14)

Поэтому если поле непосредственно перед линзой E (x, y), а поле непосредственно за линзой E¢ (x, y), то можно записать

E¢ (x, y) = E (x, y) . (10.15)

Функция t (x, y) представляет собой функцию пропускания тонкой линзы. Она является важной характеристикой линзы и широко используется при теоретическом рассмотрении применения линзы для формирования оптического изображения и для фурье-преобразования. Видим, что действие тонкой линзы на поле проходящей световой волны сводится к умножению функции распределения этого поля в плоскости XY непосредственно перед линзой на функцию пропускания линзы.

Тем самым мы показали, что действие тонкой линзы на падающую на нее световую волну можно рассматривать как действие экрана, изменяющего фазу волны (фазового экрана) в соответствии с законом (10.14).

Аналогично можно показать, что для вогнутой линзы фазовое преобразование в пренебрежении несущественной комплексной постоянной равно

t (x, y) = exp . (10.16)

Заметим, что существенная разница в фазовых преобразованиях выпуклой и вогнутой линз выражается в положительном и отрицательном знаке квадратичной фазовой задержки. Функция (10.14) описывает линзу с положительным фокусным расстоянием (f > 0), а функция (10.16) – с отрицательным фокусным расстоянием (f < 0). Поэтому первую линзу называют положительной, а вторую – отрицательной. Положительной линзой является, например, двояковыпуклая линза, а отрицательной – двояковогнутая линза. Это следует из формулы (10.13). Действительно, для двояковыпуклой линзы кривизна левой ограничивающей сферической поверхности отрицательна, а правой – положительна, т.е. 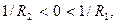и тогда Ф > 0, f > 0; для двояковогнутой линзы 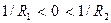и Ф < 0, f < 0.

При наложении двух линз свет проходит их последовательно: 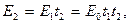т.е. функции пропускания перемножаются. Следовательно, две линзы, расположенные вплотную друг к другу, имеют функцию пропускания

t (x, y) = ,

где знак плюс относится к двум собирающим линзам, а минус – к одной собирающей, а другой рассеивающей линзам. Как видим, в системе из двух положительных линз оптические силы складываются, а в системе из положительной и отрицательной линз – вычитаются.

Такими же функциями пропускания описываются и параболические зеркала.

В прикладной оптике, кроме сферических линз, часто используют и цилиндрические линзы. Эти линзы преобразуют плоские волны в цилиндрические и наоборот. Подобно тому, как фронт цилиндрической волны получается из фронта сферической волны формальной подстановкой в формуле сферического фронта y = 0, так и функцию пропускания цилиндрической линзы можно получить, положив в функции пропускания сферической линзы y = = 0. В итоге для функции пропускания цилиндрической линзы будем иметь

t (x) = exp .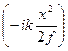

Не нашли, что искали? Воспользуйтесь поиском: