Опущен, так как он не влияет на распределение поля в плоскости X¢Y¢. Подставляя выражение в исходное соотношение (11.9) и учтя, что получим

E¢ (x¢, y¢) =

или

= .

Мы получили выражение, почти совпадающее с выражением (10.27), если в нем заменить величины с индексом 1 на величины со штрихом, а z на a. Оно показывает, что в задней фокальной плоскости линзы с точностью до множителей перед интегралом формируется фурье-спектр распределения поля в плоскости предмета. Заметим, что если предметная плоскость совпадает с передней фокальной плоскостью линзы, т.е. если a = f, то фазовый множитель перед интегралом обратится в единицу и мы получаем точное преобразование Фурье на пространственных частотах

u = x¢ / (l f), v = y¢ / (l f).

Таким образом, идеальная элементарная оптическая система позволяет получать одновременно и пространственный спектр, и изображение сигнала. В плоскости изображения формируется изображение входного сигнала, а в фокальной плоскости линзы – его спектр.

Рассмотрим теперь случай, когда предмет находится в передней фокальной плоскости линзы, т.е. когда a = f, а наблюдение распределения поля производится на произвольном расстоянии b от него. Проведя расчеты, подобные предыдущим, в предположении P = 1, для этого случая получим

=

= .

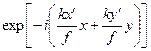Несущественный фазовый множитель здесь опущен. Распределение поля в плоскости наблюдения

=

.

В этом случае, в отличие от предыдущего, не существует однозначного соответствия между наблюдаемыми и исходными точками объекта или его спектра. Преобразуем это выражение, подставив в него обратное преобразование Фурье функции E (x, y), получим

=

+

,

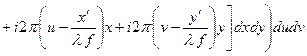где учтено, что k = 2 p / l.

Внутренний интеграл, который мы обозначим через I, можно вычислить. Используя формулу (9.21) при значениях параметров

, , ,

будем иметь

.

Учитывая это, находим

=

.

Сравнивая полученное выражение с выражением (5.12), которое в приближении когда

,

можно записать в виде

=

= .

Мы видим, что они аналогичны и с точностью до фазовых множителей перед интегралами эти выражения совпадают при условии, что

(11.16)

Используя это совпадение, можно записать

=

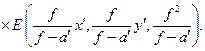
Теперь также наблюдается однозначное соответствие поля изображения с преобразованным полем предмета. Преобразование состоит в том, что изменяется масштаб поля предмета по осям X и Y в раз и оно проходит путь в свободном пространстве, определяемый величиной (11.16). Эта величина может быть больше или меньше нуля в зависимости от того, будет ли расстояние b меньше или больше фокусного расстояния линзы f.

Можно показать, что эти два рассмотренных случая (a = f и a′ = f) включают в себя все остальные случаи, в том числе и случай, когда расстояния a и b удовлетворяют формуле линзы.

Не нашли, что искали? Воспользуйтесь поиском: