Фокусирующие свойства тонкой линзы

Значение фазового преобразования, осуществляемого линзой, можно продемонстрировать на различных примерах волн, проходящих через линзу. Начнем с плоской волны, падающей на линзу параллельно ее оптической оси (оси Z). Покажем, что после прохождения через линзу плоская волна превращается в сферическую волну, сходящуюся в фокусе линзы. Пусть амплитуда плоской волны равна E ₀. Тогда поле волны, прошедшей через линзу в плоскости непосредственно за линзой найдем, умножив амплитуду плоской волны E ₀ на функцию пропускания линзы t (x, y). Получим

(10.18)

Соотношение (10.18) описывает в параксиальном приближении поле сферической волны, сходящейся в точку, расположенную на оптической оси линзы на расстоянии f от начала координат. Действительно, для поля сферической волны, исходящей из точки (x, y, 0) линзы и сходящейся в точку (0, 0, f), в параксиальном приближении имеем

E (x, y, 0) = .

Следовательно, квадратичный фазовый множитель в выражении (10.18) указывает на сходящуюся в точке сферическую волну.

В случае вогнутой линзы амплитуда E ₀ плоской волны умножается на фазовый множитель . Получающееся при этом выражение описывает в параксиальном приближении фронт сферической волны, расходящейся из точки (0, 0, – f).

Таким образом, лучи, идущие параллельно оптической оси, после преломления в положительной линзе собираются (пересе-

Рис. 7.11

каются) в одной точке F¢, расположенной на оптической оси линзы (рис. 10.2) на расстоянии f за линзой. Иными словами, тонкая положительная линза пре- образует плоскую волну в сферическую волну, сходящуюся в точке . Точка называется фокусом линзы. Линза имеет два фокуса: передний F (со стороны падающего луча – слева от линзы) и задний F¢ (со стороны преломленного луча).

Отрицательная линза преобразует параллельный пучок лучей в расходящийся. Если эти лучи продолжить в обратном направлении, то они пересекутся в точке называемой мнимым фокусом линзы (рис. 10.3). В связи с этим линзу с положительным фокусным расстоянием называют собирающей, а линзу с отрицательным фокусным расстоянием – рассеивающей. Плоская волна, не обладающая кривизной, после прохождения через положительную линзу приобретает положительную кривизну а после прохождения через отрицательную линзу – отрицательную кривизну – 1 / f.

Мы видим, что действие тонкой линзы на плоскую волну сводится к преобразованию поля этой волны в поле сферической вол-

Рис. 7.12

ны, сходящейся (для положительной линзы) в некоторой точке Fʹ (0, 0, f) за линзой или расходящейся (для отрицательной линзы) из некоторой точки F (0, 0,– f) перед линзой.

С другой стороны, линза преобразует световое поле, изображаемое точечным источником, расположенным в ее передней фокальной плоскости, в идеальную плоскую волну. Действительно, умножив поле

,

создаваемое в плоскости z = 0 и исходящее из точки S, которая находится на расстоянии f перед линзой, на функцию пропускания линзы (10.14), получим в той же плоскости z = 0 поле плоской волны с амплитудой

Амплитуда осталась прежней, так как линза меняет только фазу волны, не изменяя амплитуды. Идеальность получающейся плоской волны ограничена только апертурой линзы. (Такая линза называется дифракционно-ограниченной.)

Заметим, что это утверждение можно было бы рассматривать и как опытный факт и, основываясь на нем, получить функцию пропускания t (x, y) линзы как такую функцию, при умножении на которую комплексная амплитуда поля расходящейся сферической волны в плоскости z = 0 преобразуется в амплитуду поля плоской волны в той же плоскости.

Покажем теперь, что собирающая линза превращает сферическую волну в сферическую же волну, но с иным радиусом кривиз-

Рис. 7.13

ны. Центры кривизны этих волн представляют собой точечный объект S и его действительное изображение S¢, трактуемые с точки зрения геометрической оптики (рис. 10.4).

Действительно, пусть точка S (0, 0, – a) испускает сферическую волну. Поле, создаваемое этой расходящейся сферической волной в плоскости непосредственно перед линзой, будет . Поле за линзой найдется умножением этой функции на функцию пропускания линзы:

× = ,

где

(10.19)

Следовательно, за линзой будет распространяться сферическая волна с кривизной, определяемой соотношением (10.19). При этом, если сферическая волна, распространяющаяся залинзой, будет сходиться в точке S¢ (0, 0, а′). Если же кривизна изменит свой знак на противоположный; волна станет расходящейся из точки S¢ (0, 0, – а′). В первом случае (рис. 10.4) точка S¢ является действительным изображением точки S, а во втором – мнимым изображением. Второй случай показан на рис. 10.5.

В случае рассеивающей линзы поле в плоскости непосредственно за линзой будет

× = .

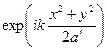Следовательно, рассеивающая линза превращает расходящуюся сферическую волну в расходящуюся же волну с кривизной

. (10.20)

Расходится эта волна не из точки S (0, 0, – a), а из точки S¢ (0, 0, – а′), являющейся мнимым изображением точки S (рис. 10.6).

Мы видим, что линзу можно рассматривать как оптический элемент, преобразующий сферическую волну одного радиуса в

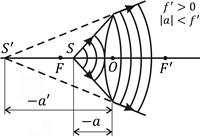Рис. 7.14

сферическую волну другого радиуса, или, иными словами, гомоцентрический (исходящий из одной точки или сходящийся в одну точку) пучок одной кривизны в гомоцентрический пучок другой кривизны. Следовательно, линза добавляет к фазе приходящего сигнала дополнительный член, соответствующий сферическому фронту волны с радиусом кривизны, равным фокусному расстоянию линзы.

Преобразование плоской волны в сходящуюся или расходящуюся сферическую волну радиуса а′ = f есть частный случай преобразования сферической волны радиуса a в сферическую волну радиуса а′, когда a = ¥.

Справедливо и обратное утверждение (этот случай рассмотрен нами выше): если на линзу падает сферическая волна с радиусом, равным фокусному расстоянию линзы (a = f), то на выходе получим плоскую волну (а′ = ¥).

Представляет интерес рассмотреть также случай, когда точечный источник света S расположен в передней фокальной плоскос-

Рис. 7.15

ти линзы на расстоянии x ₀ от оптической оси (рис. 10.7), т.е. имеет координаты x ₀, 0, – f. Сферическая волна, исходящая из этого источника, в плоскости z = 0, расположенной непосредственно перед тонкой собирающей линзой, создает поле

E (x, y) =

где

r = = ,

. В параксиальном приближении

r .

Предполагая, что x ₀ << R, а значит, R f и так как получим

r

С учетом этого для поля непосредственно перед линзой будем иметь

E (x, y) = exp .

Умножив это выражение на функцию пропускания линзы, найдем поле непосредственно за линзой:

Полученное выражение показывает, что если в передней фокальной плоскости линзы в точке S, смещенной на расстояние x ₀

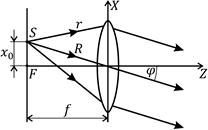Рис. 7.16

относительно оптической оси линзы, расположить точечный источник света, то за линзой будет распространяться плоская волна в направлении под углом к оптической оси линзы (к оси Z), определяемым соотношением sin𝜑 = x ₀/ R. Справедливо и обратное утверждение: плоская волна, падающая на собирающую линзу под углом к оптической оси линзы (т.е. плоская волна с пространственной частотой 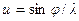), преобразуется этой линзой в сферическую волну, сходящуюся в точку S, расположенную на расстоянии x ₀ от оптической оси, т.е. в направлении, определяемом углом . Этим свойством собирающей линзы мы пользовались в главе 5 при изучении дифракции Фраунгофера. Вследствие этого свойства каждая пространственная гармоника, входящая в пространственный спектр сложного излучения, падающего на линзу, дает в задней фокальной плоскости линзы свою светящуюся точку. Совокупность этих точек и определяет пространственный фурье-спектр сложного излучения.

Собирающее и рассеивающее действия линзы можно объяснить так. Входящие в линзу участки фронта волны замедляются (так как скорость света в линзе ), происходит их задержка на величину, пропорциональную толщине линзы в данном месте. В результате этого участки фронта волны, проходящие у краев линзы, выйдут наружу раньше (для выпуклой линзы) или позже (для вогнутой линзы), чем участки, идущие посередине, и фронт волны станет вогнутым или выпуклым – волна станет сходящейся в точке F¢ или расходящейся из точки F. Точка F¢, как и точка S¢, есть точка дифракционного максимума; в эту точку волны, проходящие через разные части линзы, приходят в одинаковой фазе. Условием максимума является равенство оптических путей всех лучей, идущих через линзу в точку F¢ (или точку S¢). По современным представлениям в основе фокусирующего действия линзы лежит процесс преобразования сигнала в его спектр. Как было показано в п. 6.2, амплитуда поля в фокальной плоскости линзы пропорциональна спектральной плотности поля на входе линзы[2]. Пусть l ₁ – длина входного сигнала. Согласно соотношению неопределенностей (называемому также соотношением масштабов) пространственная частота – длина, ширина D u спектра входного сигнала обратно пропорциональна его длине l ₁: D u 1 / l ₁. Так как u = x /(l f), а x = l ₂ / 2, то D u l ₂ / (2 l f). Сравнивая оба выражения для D u, получаем l ₂ = 2 l f / l ₁. Следовательно, длина выходного сигнала l ₂ обратно пропорциональна длине входного сигнала l ₁. Поэтому если l ₁ велико, то l ₂ – мало. В этом и состоит фокусирующее действие линзы. Следует, однако, отметить, что линза не фокусирует, а модулирует по фазе падающую на нее световую волну. Фокусирующим действием обладает линза вместе с примыкающим к ней слоем свободного пространства. Таким образом, фокусирование включает в себя пространственную модуляцию (линзой) и фильтрацию (слоем свободного пространства).

Линзу по своему действию на плоскую волну можно рассматривать как зонную пластинку Френеля, поэтому отношение интенсивности в фокусе линзы к интенсивности падающей волны можно оценить по той же формуле, что и для зонной пластинки: положив в ней а′ = f и принимая в качестве R радиус линзы. Тогда при R = 0,5 см, f = 10 см и l = 0.5 мкм будем иметь I / I ₀ ~

Слой свободного пространства, линза и транспарант-диапозитив являются основными элементами когерентной оптической системы.

Фокусирующее свойство линзы определяет ее способность формировать оптическое изображение.

Относительно изображающих свойств линз необходимо отметить следующее. Если точечный источник S находится на рассто-

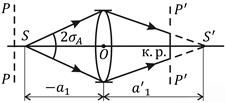Рис. 7.8

янии a ₁, не удовлетворяющем формуле линзы, то его изображение получается не в виде точки S¢, а в виде светового кружка, называемого кружком рассеяния (рис. 10.8). В случае, когда строится изображение объемного предмета, его отдельные элементы в соответствии с формулой линзы изображаются в различных плоскостях, и изображение всего предмета будет иметь пространственный характер. Однако на практике обычно изображение объемного предмета получается на плоскости (двумерном экране или на фотопластинке), поэтому только для точек предмета, которые лежат в плоскости РР, называемой плоскостью установки или плоскостью наводки, будет удовлетворяться формула линзы, а их изображение будет резким. Изображения же остальных точек предмета будут получаться в виде кружков рассеяния. Одновременно четко передать все элементы изображения объемного предмета на плоскости оказывается невозможным. Элементы предмета, расположенные на расстоянии, не удовлетворяющем формуле линзы, будут более или менее размытыми в зависимости от их удаления от плоскости изображения.

Глаз человека обладает определенной разрешающей способностью, или элементом разрешения. Это объясняет существование некоторой глубины пространства, резко отображаемого на плоскости, определяющего продольное расстояние между двумя точками предмета, размеры изображений которых на фотопленке не превышают элемента разрешения глаза. Зарегистрированное таким образом на фотопленке изображение уже нельзя превратить в трехмерное. Третье измерение можно воспринимать только за счет размытия удаленных точек предмета, за счет законов перспективы, изменения цвета и т.п.

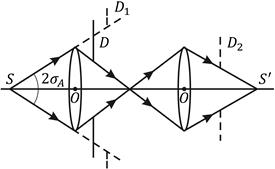
Рис. 10.9

Как видно из рис. 10.8, размер кружка рассеяния, соответствующего изображению точки S в плоскости Р¢Р′, будет тем больше, чем больше смещение S из плоскости установки РР (или из сопряженной ей плоскости Р′Р¢) и чем больше угловая ширина 2 s_А реального пучка лучей, формирующих изображение.

Для получения удовлетворительного изображения размер кружка рассеяния не должен превышать определенного предела. Глубина резкости возрастает с уменьшением угловой ширины пучка. Поэтому для уменьшения угловой ширины светового пучка (или, как говорят, для ограничения световых пучков) в оптических системах формирования изображения используются специальные диафрагмы (на рис. 10.9 диафрагма обозначена буквой D), называемые апертурными диафрагмами. Они располагаются либо между линзами, либо перед системой, либо после нее. Роль диафрагмы может играть оправа линзы (на рис. 10.9 изображена двумя вертикальными черточками). Изображение апертурной диафрагмы (действительное или мнимое), создаваемое находящейся перед ней частью оптической системы, называется входным зрачком (или входным отверстием системы), а изображение, создаваемое расположенными за диафрагмой оптическими элементами – выходным зрачком (на рис. 10.9 входной и выходной зрачки обозначены буквами D ₁ и D ₂). Входным зрачком определяется уже упоминавшаяся в п. 10.3 апертура – угол 2 s_А раскрытия пучка лучей, идущих из точки S предмета через систему.

Не нашли, что искали? Воспользуйтесь поиском: