Оптическая передаточная функция оптической системы

Применив теорему свертки к интегралу (9.39), получим для преобразования Фурье от распределения интенсивности в выходной плоскости:

I′ (u, v) = A (u, v) I (u, v), (9.41)

где I (u, v) – преобразование Фурье от распределения интенсивности на объекте, A (u, v) – преобразование Фурье от функции рассеяния точки:

A (u, v) = . (9.42)

Комплексная функция A (u, v) пространственных частот u и v называется частотным откликом оптической системы, или оптической передаточной функцией (сокращенно ОПФ) оптической системы.

К понятию оптической передаточной функции можно прийти и рассматривая, как действует линейная по интенсивности пространственно-инвариантная оптическая система на гармонический сигнал 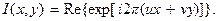Подставляя это выражение в (9.39) и опуская символ Re, получим

I¢ (x¢, y¢) = =

= . (9.43)

В полученном соотношении комплексно-амплитудный множитель A (u, v) и представляет собой ОПФ оптической системы. Это соотношение показывает, что линейная по интенсивности оптическая система действует на гармонический сигнал так же, как и оптическая система, линейная по комплексной амплитуде: гармонический сигнал на входе такой системы преобразуется в гармонический же сигнал тех же пространственных частот на выходе.

Учитывая, что F ₀(x, y) = = h (x, y) h ^*(x, y) и используя теорему умножения для преобразования Фурье, выражение (9.42) можно переписать в виде

A (u, v) = =

= =

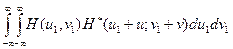= H (u, v)* H (– u, – v),

так как Полученная величина есть автокорреляция функции H (u, v). В символической форме ее можно записать так:

A (u, v) = H (u, v) H (u, v).

Следовательно, оптическая передаточная функция некогерентной оптической системы представляет собой функцию автокорреляции передаточной функции когерентной системы.

Согласно соотношению (9.41), частотный спектр распределения интенсивности в выходной плоскости оптической системы представляет собой произведение спектра частот распределения интенсивности по объекту на частотный отклик оптической системы. Мы видим, что каждой компоненте I (u, v) соответствует коэффициент (комплексный), на который эта компонента умножается при переходе от объекта к изображению. Функцию I (x, y) можно разложить в общем случае в интеграл Фурье, т.е. представить распределение интенсивности на объекте в виде совокупности бесконечного множества различных гармонических составляющих. Поэтому функция 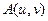определяет, каким образом каждая гармоническая составляющая спектра пространственных частот распределения интенсивности на объекте передается оптической системой, т.е. как действует оптическая система в частотной области.

Как комплексную функцию ОПФ можно представить в виде

(9.44)

Здесь модуль комплексной функции, т.е. величина 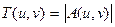, характеризует изменение амплитуды каждой гармонической составляющей спектра объекта, а аргумент – изменение ее фазы. Функцию пространственных частот называют частотно-контрастной характеристикой (ЧКХ) оптической системы, а функцию – ее частотно-фазовой характеристикой (ЧФХ), или фазовой передаточной функцией (ФПФ).

Соотношения (9.41) и (9.44) показывают, что действие линейной по интенсивности оптической системы на каждую гармоническую составляющую спектра объекта сводится лишь к изменению амплитуды и фазы этой составляющей.

Из выражения (9.42) непосредственно вытекают следующие свойства оптической передаточной функции.

1. A (0, 0) = 1. Это следует из того, что при u = v = 0 интеграл (9.39) превращается в интеграл нормировки функции (равен единице, соотношение (9.39)).

2. где A ^*(u, v) – функция, комплексно сопряженная функции A (u, v). Это следует из того, что мнимая единица i и пространственные частоты u и v входят в подынтегральную функцию (9.42) в виде произведений iu и iv, поэтому замена u на и v на 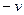эквивалентна замене i на – i, а значит, замене функции A на комплексно-сопряженную функцию A ^*.

3. Можно показать также, что | A (u, v)| £ | A (0, 0)|; ОПФ является убывающей функцией пространственных частот.

Зная ОПФ оптической системы, из (9.42) с помощью обратного преобразования Фурье можно найти функцию рассеяния точки:

F ₀(x, y) = . (9.45)

В главе 11 эта формула будет использована нами для вычисления ФРТ некоторых дифракционно-ограниченных систем (идеальных систем без аберраций, в которых имеют место только дифракционные эффекты).

Таким образом, аналогично соотношению (9.8), в случае линейных по интенсивности изопланарных оптических систем вводится некогерентная передаточная функция – ОПФ. По этой причине передаточную функцию 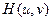часто называют когерентной передаточной функцией (КПФ) оптической системы. По аналогии с импульсной характеристикой когерентной оптической системы для систем, линейных по интенсивности, вводится функция рассеяния точки.

Существуют различные методы теоретической оценки и экспериментального определения ОПФ, но все они достаточно сложные. Только в случае дифракционно-ограниченных оптических систем со зрачками несложной формы и в пренебрежении аберрациями задача определения ОПФ системы может быть решена аналитически. Аналитические выражения ОПФ таких систем будут получены в следующей главе.

Не нашли, что искали? Воспользуйтесь поиском: