Функции рассеяния оптической системы

При оценке качества оптической системы, формирующей изображение, важно знать реакцию системы на простейшие воздействия в виде светящейся точки, линии (узкой щели) и края. Функции, описывающие распределение интенсивности на изображении точки, линии и края полуплоскости (т.е. края идеально прямолинейного ножа), называются функциями рассеяния соответственно точки, линии и края.

Введенную выше функцию, описывающую распределение интенсивности в изображении светящейся точки, – ФРТ – можно определить как интенсивность светового поля в точке (x¢, y¢) изображения, которое возникает от изображения точечного объекта, описываемого d -образной интенсивностью в точке (x, y). Действительно, полагая в интеграле суперпозиции (9.40) I (x¢ – x; y¢ – y) = d (x¢ – x; y¢ – y) и учитывая фильтрующее свойство дельта-функции, получим для интенсивности изображения в точке (x¢, y¢):

.

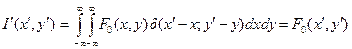Функция рассеяния точки является двумерной функцией. Это усложняет ее графическое представление и анализ. Но в некоторых случаях она упрощается. Если оптическая система обладает симметрией вращения, т.е. если отклик на точечный источник зависит только от радиуса r = , то ФРТ становится функцией одной переменной – радиуса r: F ₀(x, y) = F ₀(r). Иногда ее можно представить в виде произведения функций одной переменной (ФРТ с разделяющимися переменными):

F ₀(x, y) = F ₀₁(x)× F ₀₂(y).

Рассмотрим важный частный случай, когда заданное распределение интенсивности не зависит от координаты y. В этом одномерном случае интенсивность I (x, y) = I (x, 0); обозначим ее через I (x). Распределение интенсивности в выходной плоскости при этом также будет зависеть только от одной координаты x¢. Интеграл суперпозиции (9.40) в этом случае можно записать в виде

или

(9.46)

где функция одной переменной x

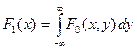(9.47)

называется функцией рассеяния линии (ФРЛ). Чтобы установить физический смысл этой функции, рассмотрим отклик линейной оптической системы на входной сигнал, описываемый d -функцией или, иначе, – на щелевой источник, параллельный оси Y. Подставив в интеграл суперпозиции (9.40) I (x¢ – x; 0) = d (x¢ – x) и учитывая фильтрующее свойство d -функции, получим

I¢ (x¢) = . (9.48)

Сравнивая это с (9.47), видим, что

F ₁(x¢) = I¢ (x¢).

К такому же соотношению можно прийти, если исходить сразу из выражения (9.46), положив в нем I (x¢ – x) = d (x¢ – x):

.

Следовательно, функция рассеяния линии F ₁(x) описывает распределение интенсивности в изображении бесконечно длинной светящейся линии (щели). По аналогии с ФРТ ее можно определить как интенсивность в точке изображения, которое возникает от изображения линейного объекта, описывающегося d -образной интенсивностью в точке x. Выражение (9.47) показывает, что функция рассеяния линии получается суммированием интенсивностей от всех точек, расположенных вдоль всей линии.

Из условия нормировки ФРТ на единицу вытекает нормировка на единицу и ФРЛ. Действительно, используя (9.39), будем иметь

.

В оптике функция рассеяния линии F ₁(x) используется чаще, чем функция рассеяния точки , так как в оптической системе бывает проще и быстрее определить отклик F ₁(x) от длинной узкой щели, чем отклик от точечного источника.

Если оптическая система имеет ФРТ с разделяющимися переменными, т.е. если можно представить в виде произведения, то на основании формулы (9.47) получаем

= ,

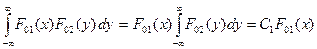где постоянная C ₁ есть значение интеграла по бесконечным пределам от функции F ₀₂(y). Аналогично можно получить для распределения интенсивности в изображении линейного источника, расположенного вдоль оси X: F ₁(y) = C ₂ F ₀₂(y), где C ₂ – значение интеграла по бесконечным пределам от функции F ₀₁(x). Постоянные C ₁ и C ₂ находятся из условия нормировки. Таким образом, функция рассеяния линии систем, имеющих ФРТ с разделяющимися переменными, с точностью до постоянного множителя равна одному из сомножителей ФРТ.

Для систем с ФРТ, обладающей круговой симметрией, отклик на щелевой источник, как и в общем случае (9.47), определится соотношением

F ₁(x) = (9.49)

т.е. находится простым интегрированием отклика F ₀(r) вдоль оси Y. Можно решить и обратную задачу: по известной ФРЛ F ₁(x) определить ФРТ F ₀(r). С этой целью приведем интеграл в (9.49) к другому виду. Поскольку подынтегральная функция

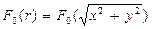
четная, то можно записать:

= 2 .

Учитывая теперь, что

,

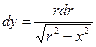
и что при изменении y от 0 до ¥ величина r пробегает значения от x до ¥, получим

F ₁(x) = 2 .

Тем самым мы пришли к преобразованию Абеля. Таким образом, функция рассеяния линии оптической системы, обладающей круговой симметрией, связана с функцией рассеяния точки этой системы преобразованием Абеля. С помощью этого соотношения и известной ФРТ можно найти ФРЛ. Обратную задачу – по известной ФРЛ найти ФРТ – тогда, очевидно, можно решить, используя обратное преобразование Абеля. Заменив в формуле (8.7) f (r) на F ₀(r) и g (x) на F ₁(x), для ФРТ оптической системы с круговой симметрией, будем иметь

F ₀(r) .

Таким образом, для оптических систем, обладающих круговой симметрией, отклик F ₁(x) на щелевой источник (ФРЛ) и отклик F ₀(r) на точечный источник (ФРТ) однозначно связаны между собой: зная одну функцию, можно найти другую функцию.

Задачу определения ФРТ по известной ФРЛ можно решить и не обращаясь к преобразованию Абеля. Введем функцию

Тогда, как можно показать,

Наличие множителя 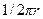связано с нормировкой функции F ₀(r).

Функция рассеяния края (ФРК) F ₂(x) описывает распределение интенсивности в изображении края светящейся полуплоскости. Предположим, что край полуплоскости совпадает с осью Y. Тогда распределение интенсивности на крае полуплоскости можно представить функцией единичного скачка (функцией Хевисайда):

(при x = 0 значение функции 1(x) полагается равным 1/2). Предполагается, что интенсивность на полуплоскости постоянна и равна единице. Заменив в выражении (9.43) на F ₂(x) и I (x¢ – x) на 1(x¢ – x), получим

F ₂(x) = , (9.50)

причем с учетом нормировки F ₁(x) значение F ₂(0) = 1/2. Графики распределения интенсивности I′ (x) на крае полуплоскости и на его изображении (т.е. ФРК F ₂(x)) показаны на рис. 9.4.

Согласно (9.50), распределение интенсивности в направлении, перпендикулярном краю полуплоскости I′ (x) = F ₂(x), описывается суммированием функций рассеяния линий в пределах полуплоскости для каждого значения координаты x:

I′ (x) = . (9.51)

Рис. 9.4

Всю полуплоскость можно мысленно разделить на отдельные линейные элементы, параллельные краю полуплоскости. Каждой

Рис. 9.5

такой светящийся линейный элемент дает свою функцию рассеяния F ₁(x). Полное изображение края образуется суммированием функций рассеяния, как это показано на рис. 9.5 для каждой точки x. На рисунке можно видеть, что т.е. сумма ординат множества функций рассеяния в данной точке x, численно равна сумме всех ординат функции рассеяния, расположенной левее точки x – для абсцисс от ¥ (так как, в принципе, функция рассеяния простирается в обе стороны до бесконечности) до x. Это и выражается формулой (9.51)

Соотношение (9.50) позволяет найти ФРК по известной ФРЛ. Используя свойство несобственных интегралов, получим обратное соотношение:

Следовательно, ФРЛ является первой производной от ФРК. С помощью этого соотношения можно найти ФРЛ по известной ФРК. Используя коммутативное свойство свертки, выражение (9.46) можно записать и в виде

Глава 6

Не нашли, что искали? Воспользуйтесь поиском: