Оптических изображений

Если световые лучи, выйдя из светящейся точки S, после прохождения через оптическую систему пересекаются в точке S¢, то точку S¢ называют оптическим изображением или просто изображением точки S. Ее называют также фокусом геометрического схождения лучей. При этом расходящаяся из точки S сферическая волна, пройдя через оптическую систему, превращается в сферическую волну, сходящуюся в точке S¢. Очевидно, что в точке S¢ будет находиться максимум интенсивности света. Каждое самосветящееся или освещенное тело можно представить как совокупность точечных источников света. Такое тело в оптике называют действительным предметом (объектом) или просто предметом (объектом). Совокупность изображений всех точек светящегося объекта представляет собой изображение этого объекта. Изображение S¢ называют действительным, если световые лучи действительно пересекаются в точке S¢, и мнимым, если в точке S¢ пересекаются продолжения лучей, проведенные в направлении, обратном распространению света. С волновой точки зрения это означает различие в знаках кривизны волновых поверхностей в направлении распространения света. Простейшим примером мнимого изображения является отражение источника S в плоском зеркале. Изображение S¢ в этом случае представляет собой точку, расположенную симметрично точке S. Действительное изображение характеризуется тем, что непосредственно освещает соответствующим образом расположенную поверхность; мнимое изображение такого освещения произвести не может. Однако при помощи оптических приспособлений мнимые изображения могут быть преобразованы в действительные. Это имеет место, например, в нашем глазу; полученное изображение освещает определенный участок сетчатки глаза.

Наряду с мнимым изображением вводится понятие и мнимого источника света. Точечный объект называется мнимым, если он является точкой пересечения продолжений действительных лучей, проведенных в обратных направлениях. Совокупность мнимых точечных источников образует мнимый предмет (мнимый объект). Если источник света S и его изображение S¢ поменять местами, то, как показывает опыт, форма всех лучей останется без изменения, но их направление изменится на противоположное. Останутся без изменения и оптические длины световых лучей. Эти утверждения носят название принципа обратимости световых лучей. Точка S¢ при этом будет играть роль источника света, а точка S – его изображения. Поэтому точки S и S¢ называют сопряженными. Аналогично, две линии или две плоскости называют сопряженными, если одна из них является оптическим изображением другой. Непрерывная совокупность точек, изображаемых оптической системой, называется пространством предмета, а непрерывная совокупность точек, являющихся их изображениями, – пространством изображения.

Когда все лучи пересекаются строго в одной точке S, изображение называется стигматическим (точечным). Пучок лучей, выходящий из одной точки или сходящийся в одну точку, называется гомоцентрическим.

Изображение называется идеальным, если любые две сопряженные кривые C и C¢ подобны друг другу. Оптическая система, дающая стигматическое (но не обязательно идеальное) изображение трехмерного предмета, называется абсолютным оптическим прибором. Для абсолютного прибора справедлива теорема Максвелла, согласно которой в абсолютном приборе оптическая длина L (C) любой кривой C в пространстве предмета равна оптической длине L (C¢) изображения C¢ этой кривой: L (C) = L (C¢). Из этой теоремы, в частности, следует, что любой треугольник и его изображение в абсолютном приборе подобны друг другу, или, что то же самое, их соответственные углы равны.

Никакие реальные оптические системы абсолютными приборами не являются. В любых оптических системах наблюдаются небольшие отклонения от идеальных условий получения изображения. Однако в теоретическом анализе часто ограничиваются рассмотрением идеальной оптической системы.

Отображения, сохраняющие неизменными углы, называют конформными. Существует общая теорема, согласно которой конформное отображение трехмерного пространства может быть только двух видов – инверсия и проективное преобразование. Поэтому отображение, создаваемое абсолютным прибором, представляет собой либо инверсию, либо проективное преобразование, либо их комбинацию. Инверсией относительно некоторой точки O называется преобразование, которое не изменяет произведение длин отрезков SO и OS¢, т.е. если SO × OS¢ = inv, где S и S¢ – пара сопряженных точек; точка O называется центром инверсии. В частности, точкой, сопряженной центру O, является бесконечно удаленная точка.

Проективное преобразование, или коллинеация, переводит точку S с координатами x, y, z в точку S¢ с координатами x¢, y¢, z¢, определяемыми соотношениями

x¢ = F ₁ / F ₀, y¢ = F ₂ / F ₀, z¢ = F ₃ / F ₀, (10.1)

где F ₀ и F_i – линейные функции координат x, y, z, т.е. F ₀ = ax + + by + cz + d и F_i = a_i x + b_i y + c_i z + d_i, где a, b, c, d, a_i, b_i, c_i, d_i – постоянные коэффициенты; i = 1, 2, 3. Значения этих коэффициентов можно определить, если известны положения начал координат и параметры оптической системы. Соотношения (10.1) устанавливают соответствие между точками пространства предметов и пространства изображений. Здесь предполагается, что точки S и S¢ относятся к разным координатным системам OXYZ и O¢X¢Y¢Z¢, начала O и O¢ которых лежат на оптической оси системы (с которой обычно совмещают ось Z) и могут не совпадать друг с другом. Если разрешить эти соотношения относительно x, y, z, получим полностью аналогичные соотношения:

x = F ₁¢ / F ₀¢, y = F ₂¢ / F ₀¢, z = F ₃¢ / F ₀¢, (10.2)

где F ₀′ и F_i¢ – линейные функции переменных x¢, y¢, z¢ c коэффициентами a¢, b¢, c¢, d′, a_i¢, b_i¢_, c_i¢, d_i¢, отличными от a, b, c, d, a_i, b_i, c_i, d_i. То, что правые части системы уравнений (10.1) являются частными от деления двух линейных функций от x, y, z, а (10.2) – функций от x¢, y¢, z¢, и обусловливает, что заданным значениям x, y, z соответствует одно, а не несколько систем значений x¢, y¢, z¢ и наоборот, заданным значениям x¢, y¢, z¢ соответствует одна система значений x, y, z. Поскольку знаменателями дробей (10.1) является одна и та же линейная функция F ₀, а знаменателями дробей (10.2) – одна и та же функция F ₀¢, плоскости

(10.3)

соответствует плоскость же

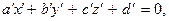(10.4)

и наоборот. В этом можно убедиться, если в уравнении плоскости (10.3) не штрихованные координаты заменить на штрихованные по формулам (10.2) или в уравнении плоскости (10.4) штрихованные координаты заменить на не штрихованные по формулам (10.1). Это справедливо и в отношении прямой линии и точки, так как прямую можно рассматривать как линию пересечения двух плоскостей, а точку – как точку пересечения трех плоскостей.

Таким образом, при проективном преобразовании каждая точка, прямая и плоскость пространства предметов изображается соответственно в виде точки, прямой и плоскости пространства изображений. Кроме того, из формулы (10.1) следует, что изображение любой точки, лежащей в плоскости F ₀ = 0, находится на бесконечности (x¢ = y¢ = z¢ = ¥, а из формулы (10.2) – что бесконечно удаленные точки проецируются на плоскость F ₀¢ = 0 (при x = y = z = ¥ получаем F ₀¢ = F ₁¢ / x = F ₂¢ / y = F ₃¢ / z = = 0). Это означает, что все лучи, вышедшие из одной и той же точки плоскости F ₀ = 0, после прохождения через оптическую систему становятся параллельными и наоборот, лучи, параллельные в пространстве предметов, после прохождения через оптическую систему пересекаются в одной и той же точке, расположенной в плоскости F ₀¢ = 0. Плоскость F ₀ = 0 называют фокальной плоскостью в пространстве предметов, или передней фокальной плоскостью оптической системы, а плоскость F ₀¢ = 0 – фокальной плоскостью в пространстве изображений, или задней фокальной плоскостью оптической системы.

Если обе фокальные плоскости находятся на бесконечности, преобразования называют аффинными или телескопическими. В этом случае коэффициенты a = b = c = 0 и a¢ = b¢ = c¢ = 0. Действительно, уравнение фокальной плоскости пространства предметов имеет вид 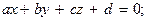x -координата этой плоскости 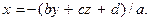Эта координата будет равна бесконечности, если 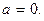Равенство бесконечности y - и z -координат требует, чтобы были равны нулю коэффициенты b и c. Аналогично доказывается равенство нулю и коэффициентов 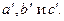Оптические системы, не имеющие фокальных плоскостей на конечном расстоянии, называются афокальными или телескопическими системами. Они являются предельными случаями обычных систем, когда обе фокальные плоскости сдвинуты в бесконечность. Всякий параллельный пучок после прохождения через такую систему остается параллельным, могут изменяться лишь ширина и направление пучка.

С математической точки зрения задача геометрической теории оптических изображений сводится к определению положения изображения при любом заданном положении предмета. В основе этой теории лежит закон прямолинейного распространения света (в однородных средах), а также законы отражения и преломления света на границе раздела сред. Следует, однако, отметить, что полная физическая теория оптических изображений должна учитывать волновые свойства света. Волновая теория позволяет более глубоко и всесторонне изучить структуру оптического изображения, оценить качество изображения, даваемого оптической системой. Как будет показано в главе 11, с точки зрения волновой природы света формирование оптического изображения можно рассматривать как результат дифракционных и интерференционных явлений, возникающих при прохождении света через объект (или при отражении от объекта) и оптическую систему.

С волновой точки зрения под оптическим изображением понимается распределение интенсивности света на плоскости, где формируется изображение. Это непосредственно связано с процессом регистрации изображения, так как любой приемник светового излучения при фиксации изображения реагирует именно на интенсивность.

Общие свойства изображающих оптических систем в геометрической теории исследуются с помощью положения, согласно которому оптические длины всех лучей, соединяющих сопряженные точки S и S¢, одинаковы. Это вытекает из того, что сферическая волна, вышедшая из точки S, превращается в сферическую же волну, сходящуюся в точке S¢, а оптические длины всех лучей от одного положения волнового фронта до другого одинаковы. Указанное положение справедливо как в отношении действительных, так и в отношении мнимых изображений, если во втором случае под лучом понимается прямолинейное продолжение его в сторону изображения S¢. Оптическая система не только изменяет знак кривизны волновой поверхности сферической волны, исходящей из каждой точки S предмета, превращая ее в сферическую волну, сходящуюся в точке S¢, но и ограничивает ее фронт. Изменение знака кривизны волновой поверхности волны соответствует фокусирующему свойству оптической системы, так как волна, выходящая из точки S, соберется в некоторой точке S¢.

Ограничение размеров волновых поверхностей световых волн с помощью оправ линз и специальных диафрагм при прохождении света через оптическую систему неизбежно приводит к возникновению дифракции. Дифракция света накладывает основное ограничение на качество изображения предмета. Она же, как будет показано в главе 11, лежит и в основе самого процесса формирования оптического изображения. Процесс образования изображения сводится к двойной дифракции: когерентный пучок света от объекта сначала испытывает дифракцию на отверстии входного зрачка, а изображение является результатом второй дифракции на выходном зрачке или, точнее, – на краях апертурной диафрагмы.

Изображаемый предмет должен быть освещен. Из опыта известно, что свет может иметь определенную окраску, вызывать различные световые ощущения, распространяться в различных направлениях. Падая на предмет, свет отражается или проходит сквозь него, причем это взаимодействие излучения и предмета влияет на само излучение. Параметры световой волны изменяются таким образом, что в них содержится информация о форме предмета, о состоянии его поверхности, о способности отдельных частей предмета поглощать и естественный белый свет и изменять его спектральный состав. Распространяясь, свет передает эту информацию объектам живой и неживой природы, которые в дальнейшем могут ее обрабатывать, регистрировать и т.п.

Глаз человека как орган зрения воспринимает световую информацию следующим образом. В выпуклой его части находится линза, которая строит изображение предмета. За глазной линзой находится система рецепторов, передающих изображение поэлементно в центральную нервную систему. Рецепторы способны быстро принять информацию об образах и передать ее для дальнейшей обработки в мозговой центр. В рецепторах информация об образе не может долго сохраняться; лишь центральная нервная система способна до определенной степени запомнить черты образа и затем воспроизвести их как представление о предмете. Эти факты лежат в основе создания оптических систем построения изображения. В этих системах используется оптический изображающий элемент, аналогичный глазной линзе. Оптическими изображающими элементами могут являться, прежде всего, линзы и зеркала.

Не нашли, что искали? Воспользуйтесь поиском: