Передаточная функция оптической системы

Понятие пространственной инвариантности позволяет ввести в рассмотрение и другую важнейшую характеристику оптической системы, называемую частотной (имеются в виду пространственные частоты) или передаточной функцией. Чтобы прийти к этой характеристике, покажем, что линейная пространственно-инвариантная оптическая система преобразует гармонический сигнал на входе в гармонический сигнал тех же пространственных частот на выходе. Действительно, пусть сигнал

E (x, y) = exp [ i 2 p (ux + vy)].

На основании коммутативного свойства свертки интеграл суперпозиции (9.6) перепишем в виде

E¢ (x¢, y¢) = . (9.7)

Подставив в (9.7) выражение гармонического сигнала, получим

E¢ (x¢, y¢) = =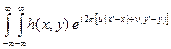

= .

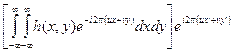Или

E¢ (x¢, y¢) = ,

где

H (u, v) = 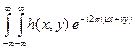. (9.8)

Тем самым мы показали, что гармонический сигнал на входе линейной пространственно-инвариантной оптической системы преобразуется в гармонический сигнал тех же пространственных частот на выходе:

= .

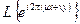Комплексную функцию H пространственных частот u и v, определяемую выражением (9.8), называют частотной или передаточной функцией оптической системы. Как видно из (9.8), передаточная функция оптической системы представляет собой фурье-образ импульсной характеристики этой системы. В этом смысле передаточная функция является сопряженной характеристикой по отношению к импульсной характеристике. Передаточная функция полностью характеризует фильтрующие свойства оптической системы. В этом смысле любую пространственно-инвариантную оптическую систему можно рассматривать как линейный фильтр пространственных частот, а прохождение сигнала через оптическую систему – как пространственную фильтрацию. Зная передаточную функцию H (u, v), c помощью обратного фурье-преобразования можно определить импульсную характеристику h (x, y):

h (x, y) = 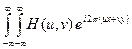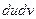. (9.9)

Частотная характеристика 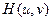является комплексной функцией, поэтому ее можно представить в виде

H (u, v) = | H (u, v)| exp [ ij (u, v)]. (9.10)

Вещественная функция 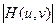при этом называется амплитудно-частотной характеристикой (АЧХ), а 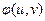– фазо-частотной характеристикой (ФЧХ) оптической системы. Часто их называют просто амплитудной и фазовой характеристиками линейной оптической системы. Соотношение (9.10) показывает, что гармонический сигнал после прохождения через линейную пространственно-инвариантную оптическую систему, не изменяя своих пространственных частот, изменяет амплитуду в 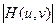раз и фазу на .

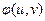Взяв преобразование Фурье от обеих частей соотношения (9.6) и воспользовавшись теоремой свертки, получим

E¢ (u, v) = E (u, v) H (u, v), (9.11)

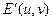где и – фурье-образы входного и выходного сигналов соответственно. Таким образом, преобразование Фурье реакции линейной пространственно-инвариантной оптической системы равно произведению фурье-преобразования входного воздействия и фурье-преобразования импульсной характеристики линейной системы. Другими словами, фурье-образ (спектр) выходного сигнала равен произведению передаточной функции оптической системы на фурье-образ (спектр) входного сигнала. Следует подчеркнуть тот факт, что если известна импульсная характеристика оптической системы, то ее преобразование Фурье является передаточной функцией этой системы.

Соотношение (9.11) позволяет заменить сложную операцию свертки простой операцией умножения пространственных спектров. Это соотношение показывает, что если сигналы в плоскости предмета и плоскости изображения представить в виде суперпозиции пространственных гармоник всех возможных пространственных частот u, v, то каждая компонента сигнала в плоскости изображения будет определяться соответствующей компонентой в плоскости предмета. Учитывая, что представляет собой разложение входного сигнала E (x, y) в виде линейной комбинации гармонических функций (гармоник) с различными пространственными частотами u и v, на основании соотношения (9.11) получаем, что при умножении на передаточную функцию 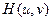учитывается действие оптической системы на каждую гармонику отдельно. Это действие, в соответствии с (9.10), сводится к изменению амплитуды и фазы каждой составляющей спектра. Согласно (9.11), сигнал передается оптической системой без искажений, т.е. E¢ (u, v) = E (u, v), если

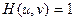(9.12)

для любых u и v. Так как фурье-образ d -функции равен единице, то равенство (9.12) имеет место, если импульсной характеристикой системы является d -функция. Равенство (9.12) может выполняться лишь для некоторых частот. Тогда эти составляющие сигнала передаются без искажений. Частоты же, для которых передаточная функция подавляются (отфильтровываются) оптической системой полностью.

Согласно определению прямого и обратного фурье-преобразований, из (9.11) следует

E (x, y) = F ^{– 1}{ E¢ (u, v)} = F ^{– 1}{ E (u, v) H (u, v)}.

Это соотношение позволяет восстановить исходную волновую информацию. Для этого следует либо зарегистрировать в произвольной плоскости пространственный спектр выходного сигнала E¢ (u, v), либо рассчитать его по результатам измерения. Затем, зная отклик или передаточную характеристику оптической системы, найти произведение 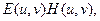обратное фурье-преобразование которого является исходным сигналом.

Так как

E¢ (x¢, y¢) = ,

то на основании соотношения (9.11) для выходного сигнала можно записать

E¢ (x¢, y¢) = 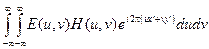. (9.13)

Выражение (9.13) показывает, что сигнал на выходе линейной оптической системы можно получить суммированием составляющих спектра входного сигнала, взятых с весом 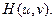Отсюда следует, что передаточная функция линейной оптической системы 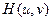является весовым множителем, определяющим относительный вклад различных составляющих спектра E (u, v) в сигнал Формула (9.13) лежит в основе так называемого спектрального метода исследования линейных оптических систем.

Таким образом, любую линейную пространственно-инвариантную оптическую систему можно рассматривать либо в пространственной области с помощью ее импульсной характеристики, либо в области пространственных частот с помощью частотной или передаточной функции. В первом случае на входе системы (в предметной плоскости) формируют сигнал от точечного излучателя, описываемого d -функцией, и анализируют функцию h (x¢, y¢) в плоскости изображения. Во втором случае на вход системы подают гармонический сигнал единичной амплитуды и наблюдают передаточную функцию системы 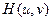. Оба подхода равноценны и выбор одного из них определяется лишь удобствами получения исходных данных о системе и простотой вычисления.

Метод спектрального разложения (спектральный метод) и метод интеграла суперпозиции используют для описания процесса прохождения сигнала через линейные оптические системы.

Покажем в заключение этого параграфа, что передаточная функция не зависит от сдвигов в координатной области. Спектральная плотность входного сигнала

= = = .

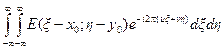Подобным образом находим спектральную плотность выходного сигнала: 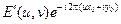. При определении отношения этих спектральных плотностей фазовый множитель exp [– i 2 p (ux ₀ + + vy ₀)] сокращается и мы получаем величину 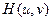, не зависящую от x ₀ и y ₀.

Не нашли, что искали? Воспользуйтесь поиском: