Решение интегрального уравнения распространения световой волны в свободном пространстве

Покажем здесь, что интегральное уравнение распространения волн (5.10)

как и интегральное уравнение (преобразование) Фурье, обладает свойством обратимости, т.е. зная распределение поля E (x, y, z) в плоскости z = const > 0, можно найти спектр исходного распределения (в плоскости z = 0), а, следовательно, и само исходное распределение E (x, y, 0). Введем оптический фильтр с передаточной функцией

(9.23)

являющейся комплексно сопряженной передаточной функции слоя свободного пространства. Пусть распределение E (x, y, z) преобразуется указанным фильтром. Действие фильтра выразится в том, что функция спектральной плотности E (u, v) умножится на частотную характеристику фильтра и тогда вместо спектральной функции E (u, v) получаем спектральную функцию

E (u, v) = E (u, v) .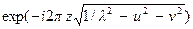

Подставляя это в уравнение (5.8)

,

получим

E (x, y, z) = =

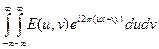= = E (x, y, 0).

Следовательно, действие фильтра, имеющего частотную характеристику вида (9.23), переводит выход во вход. Этого и следовало ожидать, так как комплексно сопряженной передаточной функции (9.23) соответствует комплексно сопряженная амплитуда плоской волны, которая описывает распространение волны в обратном направлении. Полученный результат и позволяет решить интегральное уравнение распространения волн вида (5.10).

Комплексно сопряженной передаточной функции соответствует, очевидно, и комплексно сопряженная импульсная характеристика. Для ее получения в любой формуле, определяющей импульсную характеристику слоя свободного пространства, следует заменить параметр z на – z (что соответствует замене i на – i). Тогда импульсная характеристика рассматриваемого фильтра будет иметь вид

h¢ (x, y) =

(9.24)

– в общем случае или

h¢ (x, y) = (9.25)

– в приближении Френеля. Принимая распределение E (x, y, z) за входной сигнал, а распределение E (x, y, 0) за выходной, на основании интеграла суперпозиции получим

E (x, y, 0) = .

Подставляя сюда выражение (9.15), найдем E (x, y, 0):

E (x, y, 0) =

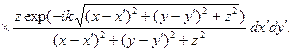
(9.26)

В приближении Френеля

E (x, y, 0) =

.

(9.27)

Соотношения (9.26) и (9.27) и решают задачу обратимости интегрального уравнения в представлении Рэлея: (9.26) – в общем случае, а (9.27) – в приближении Френеля.

Не нашли, что искали? Воспользуйтесь поиском: