
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Искажение изображения при распространении света в свободном пространстве
Пусть транспарант с изображением произвольного предмета освещается нормально падающим на него монохроматическим пучком света, например от системы лазер – расширитель пучка, создающей когерентное освещение плоской волной. Если между транспарантом и расположенным за ним экраном имеется только свободное пространство, то сходство между предметом и его изображением на экране будет весьма приблизительным, причем с увеличением расстояния все труднее в картине на экране уловить сходство с оригиналом. При распространении света в свободном пространстве теряется сходство между наблюдаемыми оптическими картинами в плоскости наблюдения (экран) и предметной плоскости (транспарант). Выясним причину этого явления.
Изображение предмета в плоскости X¢Y¢ будет определяться распределением интенсивности, а значит, и амплитуды светового поля в этой плоскости. Это поле может быть получено как сигнал на выходе слоя пространства, непосредственно примыкающего к плоскости транспаранта XY. При не слишком больших расстояниях  между плоскостями XY и X¢Y¢ это поле определится преобразованием Френеля:
между плоскостями XY и X¢Y¢ это поле определится преобразованием Френеля:
E¢ (x¢, y¢) =
= 
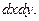 (11.1)
(11.1)
Этот интеграл свертки позволяет объяснить, почему распространение света в свободном пространстве приводит к искажению изображения. Видно, что поле E¢ в любой точке  плоскости наблюдения X¢Y¢ с точностью до несущественных множителей перед интегралом получается суммированием полей от всех точек (x, y) предметного поля, помноженных на фазовый множитель, квадратично зависящий от координат точек предметного поля. Наличие этого множителя и приводит к искажению изображения.
плоскости наблюдения X¢Y¢ с точностью до несущественных множителей перед интегралом получается суммированием полей от всех точек (x, y) предметного поля, помноженных на фазовый множитель, квадратично зависящий от координат точек предметного поля. Наличие этого множителя и приводит к искажению изображения.
Процессы, связанные с искажением изображения в свободном пространстве, удобно рассматривать, перейдя в пространство фурье-координат или, иначе, в область пространственных частот u и v. Произведя преобразование Фурье соотношения (11.1) и учтя теорему свертки, получим

=  , (11.2)
, (11.2)
где  и
и  – фурье-образ распределения поля в плоскости предмета и плоскости наблюдения соответственно, произведение двух последних сомножителей представляет собой передаточную функцию
– фурье-образ распределения поля в плоскости предмета и плоскости наблюдения соответственно, произведение двух последних сомножителей представляет собой передаточную функцию 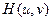 свободного пространства в приближении Френеля. Из (11.2) видно, что действие свободного пространства приводит к изменению фазы плоских волн, достигающих плоскости наблюдения, на величину, пропорциональную квадратам пространственных частот u и v, причем это изменение будет тем больше, чем больше расстояние
свободного пространства в приближении Френеля. Из (11.2) видно, что действие свободного пространства приводит к изменению фазы плоских волн, достигающих плоскости наблюдения, на величину, пропорциональную квадратам пространственных частот u и v, причем это изменение будет тем больше, чем больше расстояние  от плоскости предмета до плоскости наблюдения (линейный фазовый множитель
от плоскости предмета до плоскости наблюдения (линейный фазовый множитель 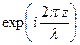 на распределение частот не влияет). Это обстоятельство является определяющим для искажения изображения предмета, так как фазовые соотношения между слагаемыми плоскими волнами в плоскости предмета и плоскости наблюдения, отстоящей на расстояние z, различны. Различие фазовых соотношений приводит к различию результатов интерференции составляющих плоских волн. Поэтому результирующее распределение поля в плоскости наблюдения будет кардинально отличаться от распределения поля в плоскости предмета. Отметим, что это различие, а значит, и величина искажения изображения будут зависеть от расстояния z от предмета до плоскости наблюдения.
на распределение частот не влияет). Это обстоятельство является определяющим для искажения изображения предмета, так как фазовые соотношения между слагаемыми плоскими волнами в плоскости предмета и плоскости наблюдения, отстоящей на расстояние z, различны. Различие фазовых соотношений приводит к различию результатов интерференции составляющих плоских волн. Поэтому результирующее распределение поля в плоскости наблюдения будет кардинально отличаться от распределения поля в плоскости предмета. Отметим, что это различие, а значит, и величина искажения изображения будут зависеть от расстояния z от предмета до плоскости наблюдения.
Проиллюстрируем сказанное на следующем примере. Пусть предметом является одномерная амплитудная гармоническая решетка с функцией пропускания

где коэффициенты t 0 и t 1 удовлетворяют тем же условиям, что и в соотношении (7.1). При освещении решетки плоской волной амплитуды E 0 распределение светового поля непосредственно за плоскостью предмета (при z = 0) можно представить в виде
E (x) = E 0 t 0 +  E 0 t 1
E 0 t 1 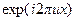 +
+  E 0 t 1
E 0 t 1 
Данному граничному условию соответствует в свободном пространстве за предметом световое поле из трех плоских волн
E (x, z) = E 0 t 0  +
+  E 0 t 1exp[ i 2 p (ux + wz)] +
E 0 t 1exp[ i 2 p (ux + wz)] +
+  E 0 t 1 exp[ – i2p (ux – wz)].
E 0 t 1 exp[ – i2p (ux – wz)].
Считая, что u << 1 / l, пространственную частоту w представим в виде  Тогда для поля в плоскости X¢Y¢ получим
Тогда для поля в плоскости X¢Y¢ получим
E (x¢, z) = E 0 t 0 exp(i 2 p z / l) +  E 0 t 1 exp[ i 2 p (ux¢ + z / l –
E 0 t 1 exp[ i 2 p (ux¢ + z / l –
–  l z u 2)] +
l z u 2)] +  E 0 t 1 exp[– i 2 p (ux¢ – z / l +
E 0 t 1 exp[– i 2 p (ux¢ – z / l +  l z u 2)] =
l z u 2)] =
= E 0 exp(i 2 p z / l){ t 0 +  t 1 E 0exp(– ipl z u 2)
t 1 E 0exp(– ipl z u 2) 
 [exp(i
[exp(i  ) + exp(– i
) + exp(– i  )]}.
)]}.
Применив к выражению в квадратных скобках формулу Эйлера, для поля в плоскости X¢Y¢ будем иметь
E¢ (x¢, z) = E 0exp(i 2 p z / l)[ t 0 +
+ t 1exp(– ipl z u 2) 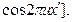 (11.3)
(11.3)
Выражение (11.3) показывает, что гармоническая составляющая функции пропускания решетки на пространственной частоте u умножается на квадратичный фазовый множитель exp(– ipl zu 2).
Распределение интенсивности в плоскости наблюдения
I (x¢, z) ~  =
=  [ t 0 2 + 2 t 0 t 1
[ t 0 2 + 2 t 0 t 1 

 cos pl z u 2 + t 12
cos pl z u 2 + t 12 
Полученное выражение отличается от распределения интенсивности в плоскости предмета
I (x¢, 0) ~ 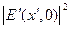 =
=  [ t 0 2 + 2 t 0 t 1
[ t 0 2 + 2 t 0 t 1  +
+
+ t 1 2 
фазовым множителем  Этот множитель равен единице при z, удовлетворяющих условию
Этот множитель равен единице при z, удовлетворяющих условию  = 2 p m (m = 0, 1, 2, 3,…), т.е. при
= 2 p m (m = 0, 1, 2, 3,…), т.е. при
 (11.4)
(11.4)
где d = 1 / u – пространственный период решетки. В этом случае распределение интенсивности светового поля в плоскости наблюдения 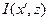 будет в точности совпадать с распределением интенсивности светового поля в плоскости предмета
будет в точности совпадать с распределением интенсивности светового поля в плоскости предмета  – изображение получается полностью идентичным предмету. На расстояниях z, не удовлетворяющих условию (11.4), изображение будет в большей или меньшей степени отличаться от предмета, т.е. будет искаженным. Следовательно, если экран перемещать вдоль оси Z, изображение решетки на экране будет то появляться, то исчезать с периодичностью
– изображение получается полностью идентичным предмету. На расстояниях z, не удовлетворяющих условию (11.4), изображение будет в большей или меньшей степени отличаться от предмета, т.е. будет искаженным. Следовательно, если экран перемещать вдоль оси Z, изображение решетки на экране будет то появляться, то исчезать с периодичностью
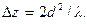
Это явление, впервые описанное Талботом, называют эффектом самовоспроизведения. Заметим, что D z определяется квадратом пространственного периода решетки. Это является следствием нелинейности фазовой характеристики свободного пространства по пространственным частотам u и v.
Если транспарант имеет произвольную функцию пропускания t (x), то ее можно разложить в ряд или в интеграл Фурье, т.е. представить транспарант в виде конечного или бесконечного числа гармонических решеток с различными периодами d = 1 / u. Плоские волны от каждой такой решетки, распространяясь за транспарантом, будут давать их изображения на расстояниях вдоль оси Z, определяемых формулой (11.4). Однако в общем случае за транспарантом не будет такой плоскости, где все решетки дают свои изображения в фазе – изображение предмета будет искаженным.
Таким образом, искажение изображения предмета происходит из-за тех фазовых искажений, которые появляются при распространении световых волн в свободном пространстве между транспарантом и экраном. Восстановить изображение – это значит скомпенсировать эти искажения. Такая компенсация в оптике осуществляется при помощи линз, зонных пластинок или голографическим методом. Линза с соответствующим фокусным расстоянием и соответствующим образом расположенная между предметом и экраном так воздействует на фазу световых волн, что фазовые искажения компенсируются с избытком и только действие свободного пространства за линзой приводит к восстановлению изображения. Это согласуется с тем, что, как было отмечено в предыдущем параграфе, фокусирующим, а значит, и изображающим свойством обладает линза вместе с примыкающим к ней слоем свободного пространства. Линза компенсирует таким образом действие свободного пространства между предметом и линзой и между линзой и изображением, что и отражено в формуле линзы, связывающей между собой фокусное расстояние линзы с толщинами слоев свободного пространства, расположенных перед линзой и за линзой. Однако, как мы увидим ниже, из-за конечных размеров линзы и возникающей вследствие этого дифракции на оправе линзы изображение предмета, даваемое линзой, не будет полностью идентично самому предмету. Оно будет несколько размытым, нечетким.
6.5. Изображение линзой точечного объекта
Пусть на оптической оси Z в начале координатной плоскости XY на расстоянии a от линзы имеется точечный источник света S. Будем последовательно определять распределение комплексных амплитуд поля в различных плоскостях оптической системы по ходу распространения световой волны от этого источника (вдоль положительного направления оси Z). В плоскости XY непосредственно за источником S он создает распределение поля, описываемое d -функцией:
E (x, y) = E 0 d (x, y). (11.5)
В плоскости непосредственно перед линзой распределение поля можно найти с помощью преобразования Френеля (11.1), подставив в него выражение (11.5) и заменив в нем x′ и y′ на координаты в плоскости линзы  и
и 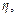 а z на a:
а z на a:
E 1(x, h) =  .
.
Учитывая фильтрующее свойство d -функции, получим
E 1(x, h) =  exp
exp  .
.
Заметим, что такое же поле в плоскости xh, т.е. в плоскости z = a, создавала бы расходящаяся сферическая волна с комплексной амплитудой
E (x, y) =  exp
exp 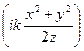 .
.
Это подтверждает возможность представления точечного источника света, создающего расходящуюся сферическую волну, δ -функцией.
Поле в плоскости непосредственно за линзой определится умножением поля непосредственно перед линзой E 1(x, h) на функцию пропускания линзы  . Конечные размеры линзы учтем умножением t (x, h) на зрачковую функцию линзы P (x, h). Учитывая это, находим
. Конечные размеры линзы учтем умножением t (x, h) на зрачковую функцию линзы P (x, h). Учитывая это, находим
E 1¢(x, h) =  exp
exp 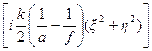 .
.
Поле в плоскости X¢Y¢ на расстоянии a′ от линзы найдется с помощью преобразования Френеля
E¢ (x¢, y¢) = 
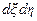 .
.
Возведя в квадрат выражения в круглых скобках в показателе экспоненты, подставив значение E 1′ 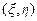 и сгруппировав члены, получим
и сгруппировав члены, получим
E¢ (x¢, y¢) = 


Так как зрачковая функция P (x, h) равна нулю вне апертуры линзы, то интегрирование проводится в бесконечных пределах. Будем считать, что a и  удовлетворяют формуле линзы
удовлетворяют формуле линзы

В этом случае плоскость X¢Y¢ является плоскостью изображения. Тогда квадратичный фазовый множитель в подынтегральном выражении выпадает (обращается в единицу). Учитывая далее, что

 ,
,
для поля в плоскости изображения X¢Y¢ будем иметь:
E′ (x¢, y¢) =
= 

(11.6)
Предположим теперь, что P (x, h) = 1, т.е. радиус линзы достаточно велик, так что все лучи, исходящие из источника S, проходят через линзу. В этом случае интеграл
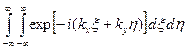
в (11.6) будет представлять собой фурье-образ единицы. Последний равен d -функции, умноженной на 

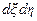 =
= 
 =
=
=  d
d  .
.
Поскольку изображение наблюдают или регистрируют в виде распределения интенсивности, а при определении интенсивности фазовый множитель в комплексной амплитуде выпадает, то фазовые множители в (11.6) можно положить равными единице. Тогда получим
E (x¢, y¢) = 

 .
.
Правая часть этого выражения обращается в нуль всюду, кроме точки с координатами x¢ = y¢ = 0. Отсюда видно, что падающая на линзу сферическая волна сходится в плоскости изображения в математическую точку с координатами x¢ = y¢ = 0, z = a + a′.
Таким образом, даваемое линзой неограниченных размеров изображение точечного объекта, расположенного на оптической оси (оси Z) на расстоянии a от линзы, представляет собой геометрическую точку, расположенную на расстоянии a′ от линзы, причем расстояния a и a′ связаны между собой формулой линзы. Следовательно, формула линзы описывает условие, при котором сферическое световое поле будет сходиться и воспроизводить изображение точечного объекта в плоскости изображения. Полученный результат полностью согласуется с геометрической теорией изображения, согласно которой точка в пространстве предметов изображается идеальной линзой в виде точки в пространстве изображений. На языке волн это означает, что идеальная линза превращает сферическую изофазную поверхность предметной волны в сферическую поверхность изображающей волны с иным радиусом кривизны. Центры кривизны этих волн представляют собой точечный объект и его изображение, трактуемое с точки зрения геометрической оптики.
6.6. Изображение линзой протяженного предмета
Предположим теперь, что в плоскости XY расположен транспарант, функция пропускания которого t (x, y). Транспарант освещается плоской монохроматической волной c комплексной амплитудой  В плоскости непосредственно за транспарантом эта волна создает световое поле E (x, y) = E 0 t (x, y). Оптическая система, содержащая модулирующий элемент (в нашем случае транспарант), слой свободного пространства, собирающую сферическую линзу и затем снова слой свободного пространства, называется элементарной оптической системой или оптическим каскадом. Для расчета распределения поля в плоскости изображения X′Y′ оптический каскад удобно представить в виде двух последовательно соединенных линейных систем, для каждой из которых сигнал на выходе соответствует распределению поля в области дифракции Френеля. Функциональная схема процесса образования изображения показана на рис. 11.1.
В плоскости непосредственно за транспарантом эта волна создает световое поле E (x, y) = E 0 t (x, y). Оптическая система, содержащая модулирующий элемент (в нашем случае транспарант), слой свободного пространства, собирающую сферическую линзу и затем снова слой свободного пространства, называется элементарной оптической системой или оптическим каскадом. Для расчета распределения поля в плоскости изображения X′Y′ оптический каскад удобно представить в виде двух последовательно соединенных линейных систем, для каждой из которых сигнал на выходе соответствует распределению поля в области дифракции Френеля. Функциональная схема процесса образования изображения показана на рис. 11.1.

Рис. 11.1
В результате прохождения первого свободного пространства протяженностью a поле в плоскости непосредственно перед линзой определится преобразованием Френеля
E 1(x, h) = 
(11.7)
Не нашли, что искали? Воспользуйтесь поиском: