Влияние на изображение конечных размеров

Линзы

Будем считать теперь, что линза имеет конечный радиус R. Рассмотрим опять сначала точечный объект, расположенный на расстоянии a от линзы. Если a и a′ связаны между собой формулой линзы, то в соответствии с выражением (11.6) определение распределения поля в плоскости изображения сводится к вычислению интеграла

I = ,

т.е. к фурье-преобразованию зрачковой функции линзы. Зрачковая функция имеет такой же вид, как и апертурная функция круглого отверстия, поэтому можно воспользоваться результатом, полученным при рассмотрении дифракции Фраунгофера на круглом отверстии. В п. 6.7 было показано, что

I (a) = I (0) . (11.18)

Здесь – функция Бесселя первого рода первого порядка,

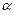= Rk _^ = R ,

или, учитывая, что

= , = .

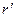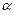Функция показана на рис. 6.8. Она имеет максимум при 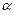= 0, т.е. при 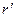= 0. Первый минимум этой функции достигается при 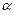= 3,83, т.е. на расстоянии 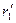= 0,61 l a′ / R от начала координат плоскости X¢Y¢, расположенного на оптической оси линзы. Отсюда следует, что в отличие от линзы с бесконечными размерами, которая фокусирует плоскую волну в математическую точку (дельта-функция в выражении (11.5)), линза с конечным радиусом R преобразует падающую на нее часть плоской волны в пятно конечной ширины. Изображение точечного источника, даваемое линзой конечных размеров, не является точечным, как это было в случае неограниченной линзы, а размывается в целую дифракционную картину в виде светового кружка (кружка Эри) радиусом 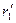, окруженного чередующимися темными и светлыми кольцами. Центр дифракционной картины расположен на оси линзы в точке идеального изображения x¢ = y¢ = 0.

Выражение (11.18) можно получить и рассматривая образование распределения поля в плоскости изображения как результат двойной дифракции световой волны от плоскости объекта до плоскости зрачка линзы и от плоскости зрачка до плоскости изображения. Так как оптическая система предполагается идеальной, дифракцию можно считать фраунгоферовской. Более точно распределение поля на зрачке соответствует фурье-образу распределения поля на входной плоскости. Следовательно, распределение поля в плоскости изображения найдется как

= F ^{– 1}{F{ E (x, y)} P (x, h)},

где F – обозначение фурье-преобразования с ядром exp , P (x, h) – функция зрачка линзы. Отсюда для точечного источника, расположенного в начале координат (x = 0, y = 0), будем иметь

= F ^–1{F{ d (x, y)} P (x, h)} = C .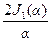

Как уже отмечалось в п.6.7, изображение точки в виде пятна конечных размеров является следствием ограничения фронта падающей на оптическую систему световой волны, обусловленного конечными поперечными размерами диафрагмы и самой линзы. На краях диафрагмы или на оправе (на апертуре) линзы возникает более или менее заметная дифракция. Световая волна после дифракции на линзе будет создавать в фокальной плоскости линзы или в плоскости, где возникает изображение источника света, дифракционную картину. В этом отношении линза конечных размеров ведет себя подобно круглому отверстию в непрозрачном экране при дифракции Фраунгофера. Таким образом, дифракция света ставит определенный предел получению стигматического изображения. Никакая, даже самая совершенная линза не дает идеального изображения, изображением точки будет являться не точка, а целая дифракционная картина Эри. Распределение интенсивности света в окрестности точки, соответствующей геометрическому изображению, определяется как результат интерференции когерентного света, исходящего из каждой точки волновой поверхности волны, прошедшей сквозь линзу (или выходной зрачок идеальной оптической системы) и являющейся, согласно принципу Гюйгенса – Френеля, источником когерентного излучения. Величину 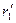можно считать мерой степени неопределенности, с которой точка в плоскости пространственных частот (в фокальной плоскости линзы) соответствует пространственной частоте аксиальной плоской волны, падающей на линзу конечного радиуса R. Эта неопределенность является следствием того, что линза конечных размеров собирает лишь часть пространственной информации, которую несет световая волна.

В более общем случае, при наличии аберраций (недостатков) линз и других причин, даваемое линзой изображение точечного источника (или, как говорят, отклик системы на точечное (импульсное) воздействие) будет представлять собой световое пятно с изменяющейся от точки к точке интенсивностью, которое называется функцией рассеяния точки (ФРТ) оптической системы[3].

Чтобы найти связь между распределением амплитуд и E (x, y) в случае объекта конечных размеров, обратимся снова к соотношению (11.13). Перейдем в этом соотношении к новым переменным: b x = – s, b y = – t. Тогда получим

h (x, y, x¢, y¢) =

= .

В новых переменных функция отклика системы h (x, y, x¢, y¢) зависит только от разности координат. Если ввести в рассмотрение функцию

(x¢ – s, y¢ – t) = h (x, y, x¢, y¢),

то интеграл суперпозиции (11.9) с учетом замены переменных можно привести к виду

= ,

где

(x, y) =

(11.19)

Полученное выражение для представляет собой свертку импульсной характеристики системы с идеальным изображением. Оно и определяет связь между распределением комплексных амплитуд светового поля в плоскости предмета и плоскости изображения с учетом ограниченных размеров линзы. Как видим, учет конечных размеров апертуры линзы приводит к замене однозначного соответствия между точками предмета и изображения преобразованием свертки.

Таким образом, изображение, даваемое линзой, не является точной копией предмета. Поскольку это изображение определяется сверткой, а при свертке каждая точка входной функции, описываемой d -функцией, расширяется на выходе в пятно (кружок Эри), то оно является несколько размытым, неконтрастным. Физической причиной этой размытости и неконтрастности является дифракция света на апертуре линзы.

Кроме дифракционных эффектов, на качество изображения существенное влияние оказывают и различные аберрации (недостатки) линз, полное устранение которых оказывается практически невозможным.

Для рассмотрения вопроса о влиянии конечных размеров апертуры линзы на распределение поля в задней фокальной плоскости линзы положим в формуле (11.11) а′ = f. В этом случае импульсная функция примет вид

h (x, y, x¢, y¢)

Подставим это выражение в формулу (11.9). После некоторых несложных преобразований эту формулу приведем к виду

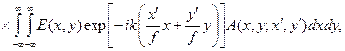
где

и несущественный множитель опущен. Показатель экспоненты, стоящей под знаком интеграла в выражении имеет вид квадратичной формы. Кроме того, апертурная функция P (x, h) для типичных для оптики значений l является медленно меняющейся, поэтому для вычисления второго интеграла можно воспользоваться методом стационарной фазы.

Согласно этому методу, если F (x) – медленно меняющаяся функция, то

,

где x ₀ – корень уравнения f ¢(x) = 0. В двумерном случае для медленно меняющейся функции F (x, h) будем иметь

где x ₀, h ₀ – корни системы уравнени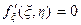й , Знаки под корнем в знаменателях правых частей поставлены для того, чтобы обеспечить положительность подкоренных выражений. Отметим также, что под медленно меняющейся функцией понимается функция, медленно меняющаяся в интервале шириной

D x

в одномерном случае и в интервалах изменения переменных x, h шириной

D x , D h

соответственно в двумерном случае.

Применяя вторую формулу вычисления интеграла по методу стационарной фазы к выражению 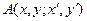и учтя, что в нашем случае

, , ,

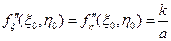получим

.

Фазовый множитель exp опущен как несущественный. Ширина интервалов, в которых апертурная функция должна медленно изменяться D x = D h = 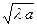. Ввиду малости l эти величины меньше интервалов изменения переменных x и h, в пределах которых апертурная функция остается постоянной, равной единице, поэтому условие применимости метода стационарной фазы к вычислению выражения выполняется. С учетом этого находим распределение комплексной амплитуды поля в задней фокальной плоскости линзы:

. (11.20)

Поскольку координаты x¢ и y¢ связаны с пространственными частотами u и v соотношениями x¢ = l f u и y¢ = l f v, то формулу (11.20) можно записать в следующем виде:

.

Из полученного соотношения видно, что при учете влияния ограниченного размера зрачка линзы поле в задней фокальной плоскости линзы и поле в плоскости предмета не связаны преобразованием Фурье. Лишь при a = 0, когда предмет расположен вплотную к линзе и его физические размеры меньше диаметра зрачка линзы, влиянием зрачка можно пренебречь. В этом случае с точностью до квадратичного фазового множителя указанные поля будут связаны преобразованием Фурье.

Не нашли, что искали? Воспользуйтесь поиском: