Образование изображения при когерентном освещении как двойное преобразование Фурье

Покажем, что комплексная амплитуда светового поля в плоскости изображения связана с комплексной амплитудой в плоскости предмета через два преобразования Фурье (прямого и обратного). Для этого рассмотрим снова процесс образования изображения элементарной оптической системой. Как и прежде, будем считать линзу неограниченной, поэтому интегрирование будем проводить в бесконечных пределах.

Световое поле в плоскости непосредственно перед линзой определится сверткой функции предмета E (x, y) с импульсным откликом свободного пространства перед линзой:

E ₁(x, h)= =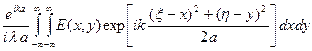

=

. (11.17)

В конечном выражении фазовый множитель одинаковый для всех точек (x, h) и учитывающий только набег фазы при распространении света от плоскости предмета до плоскости линзы, опущен. Интеграл (11.17) представляет собой преобразование Фурье от функции E (x, y)exp на пространственных частотах

Введем обозначение

F = F .

С учетом этого для поля непосредственно за линзой можно записать выражение

E ₁¢(x, h) = E ₁(x, h) exp =

= F exp =

= F ,

где учтено также, что в соответствии с формулой линзы

1 / a – 1 / f = 1 / a′.

Поле в плоскости изображения определится сверткой функции E ₁¢(x, h) с импульсным откликом второго свободного пространства:

= =

=

=

В этом выражении фазовый множитель опущен как не влияющий на распределение амплитуды поля в плоскости X¢Y¢

Перейдем к новым переменным

Тогда

=

Интеграл в этом выражении является обратным фурье-преобразованием функции 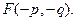Учитывая свойство фурье-преобразований и заменив в функции f (x, y) = E (x, y) exp переменные x, y соответственно на получим

=

=

= =

= ,

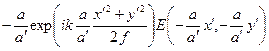где b = a′ / a – коэффициент увеличения линзы. При получении этого выражения мы снова учли формулу линзы и что k = 2 p / l. Квадратичный фазовый множитель определяет фазовые искажения изображения. При

указанный фазовый множитель можно положить равным единице, и тогда

= .

Мы снова пришли к выражению (11.14).

Тем самым мы показали, что распределение комплексной амплитуды в изображении представляет собой двойное преобразование Фурье:

= F^-1{F{ E (x, y)}× t (x, y)}.

Это можно проиллюстрировать и на эквивалентной оптической схеме, приведенной на рис. 10.2. Амплитуда волны в задней фокальной плоскости первой линзы равна фурье-образу амплитуды в плоскости предмета, а амплитуда волны в плоскости изображения в свою очередь является фурье-образом амплитуды волны света в задней фокальной плоскости первой линзы. Процесс образования изображения можно рассматривать и как последовательность двух процессов дифракции Фраунгофера, описываемой преобразованием Фурье.

Не нашли, что искали? Воспользуйтесь поиском: