Формирование оптического изображения

По Аббе – Портеру

Существуют две модели формирования оптического изображения, каждая из которых наиболее удачно применяется в совершенно определенных условиях. Согласно первой модели (модели Аббе – Портера), образование изображения при когерентном освещении сводится к образованию дифракционной картины в фокальной плоскости линзы и последующему суммированию в плоскости изображения интерференционных полос, создаваемых лучами, проходящими через пары дифракционных максимумов m -го порядка, но с непрерывным диапазоном разнесения полос и их ориентацией. Или к двойному преобразованию Фурье (так как образованию фраунгоферовской дифракционной картины соответствует преобразование Фурье от функции амплитудного распределения по объекту, а суммированию интерференционных полос – суммирование фурье-компонент). Согласно второй модели (модели Рэлея), применяемой для описания формирования изображения, как при когерентном, так и при некогерентном освещении, изображение протяженного объекта можно представить как комбинацию элементарных изображений, которые оптическая система создает отдельно для света от каждой точки объекта. Если освещение когерентно, то имеет место интерференция и тогда изображение математически можно представить в виде комбинации элементарных изображений с комплексными амплитудами. В этом случае при представлении объекта в виде последовательности равно разнесенных точечных источников для описания суммирования регулярно расположенных элементарных изображений, формирующих изображение объекта, можно использовать ряды Фурье. При этом члены рядов соответствуют порядкам дифракции модели Аббе – Портера. Если же освещение не когерентно, то в плоскости изображения будут суммироваться не амплитуды, а интенсивности элементарных изображений, полученные от каждой точки объекта. Рассмотрим здесь первую модель подробно. Вторая модель будет описана в п. 12.4.

Предположим сначала, что объектом является дифракционная решетка РР, освещаемая параллельным пучком монохроматических лучей. Изображение решетки создается в плоскости Р¢Р¢ (рис. 11.4). Вследствие дифракции на решетке свет, прошедший через решетку, будет состоять из дискретного ряда плоских дифрагировавших волн, распространяющихся от решетки по различным направлениям. В фокальной плоскости F линзы L возникает фраунгоферова дифракционная картина в виде набора ярких точек – дифракционных максимумов различных порядков. В точке пересечения этой плоскости с оптической осью линзы находится максимум нулевого порядка M ₀ (m = 0), по обе стороны от которого располагаются максимумы первого и (m = 1), второго и (m = 2), третьего 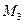и (m = 3) и т.д. порядков согласно формуле d sin j_m = ml, где d – период решетки. Интенсивность этих максимумов убывает по мере того, как увеличивается их порядок.

Рис. 11.4

Совокупность точек и т.д. Э. Аббе назвал первичным или дифракционным изображением. Эти точки – дифракционные максимумы – являются источниками вторичных когерентных волн Гюйгенса, которые, распространяясь далее за фокальной плоскостью FF, встречаются в сопряженной с Р плоскости изображения Р¢Р¢. Интерферируя между собой, эти вторичные волны в плоскости Р¢Р¢ создают дифракционную картину, называемую вторичным изображением Аббе, которая и представляет собой более или менее точное изображение решетки. При этом линза выполняет задачу сведения дифрагировавших на решетке световых пучков в плоскости изображения. Процесс распространения света от фурье-плоскости до плоскости изображения Аббе назвал второй дифракцией. Таким образом, формирование оптического изображения решетки происходит в две стадии: на первой (предварительной) стадии происходит дифракция света на решетке с образованием фраунгоферовской дифракционной картины в фокальной плоскости линзы, а на второй (окончательной) – рекомбинация дифрагированного света (отклоненных пучков) линзой в реальное изображение. Отметим, что если на рис.11.4 выделить два луча, идущих, например, из точки О ₁ в точку О ₁ ′, один проходящий через центр линзы, другой – через ее нижний край, то мы увидим, что здесь нет противоречия между этим волновым описанием и методом лучей геометрической оптики.

Взятая сама по себе любая пара максимумов 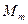и создает интерференционную картину на плоскости изображения. Это напоминает интерференционный опыт Юнга, в котором пара узких отверстий в непрозрачном экране действует таким же образом. Интерференционную картину в опыте Юнга часто называют дифракционной картиной, имея в виду физический процесс (дифракцию), при котором свет проходит через каждое отверстие, чтобы попасть к месту интерференции. В этом смысле формирование изображения можно рассматривать как двойной процесс дифракции (идея, принадлежащая Цернике).

Чтобы уяснить, каким способом строится изображение объекта типа решетки, показанной на рис. 11.4, рассмотрим вклады в изображение, вносимые парами дифрагировавших лучей, включающих различные порядки дифракции, т.е. вклады, которые вносят пары максимумов , m = 1, 2, 3, … На рис. 11.5 показана схема образования пары дифрагировавших лучей m -го порядка, испускаемых решеткой. В плоскости изображения Р¢Р¢ они интерферируют, создавая распределение интенсивности по гармоническому закону с периодом d¢_m, равным ширине интерференционной полосы h.

Рассматривая дифракционные максимумы как когерентные источники, для определения ширины полосы h воспользуемся формулой (3.25) где a – расстояние между источникам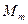и и , l – расстояние от источников и до плоскости Р¢Р¢, в которой наблюдается интерференционная картина. С помощью рис. 11.5 находим где 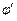– угол схождения интерферирующих лучей, т.е. угол, под которым из точки О¢ ₁ виден отрезок длиной а, соединяющий источник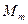и и , а так как j¢ – мал, то можно считать, что Следовательно,

d¢_m = h ≈ l / sin j¢.

С другой стороны, условием для формирования максимумов m -го порядка от дифракционной решетки является выражение d sin j = = ml. С учетом этого получаем связь между периодом d¢_m гармонического распределения интенсивности, создаваемым парой максимумов m -го порядка, и периодом решетки d:

d¢_m ≈ (d / m)×(sin j / sin j¢).

Множитель во вторых скобках является постоянным по величине и связан с увеличением линзы, поэтому имеем: d¢_m ~ d / m.

Рис.11.5

Волны, проходящие через максимумы первого порядка, интерферируют в плоскости изображения Р¢Р¢, создавая в этой плоскости гармонические осцилляции интенсивности, которые соответствуют основному периоду решетки (d¢_m ~ d). Этот период дает минимальную информацию об изображаемом объекте (решетке) без тонких деталей его оптической структуры. Каждая пара последующих максимумов более высокого порядка добавляет последовательно к общему распределению интенсивности гармоники (колебания интенсивности) более короткого периода (d¢_m ~ ~ ), которые формируют изображение.

Аббе продемонстрировал это, перекрывая с помощью различных экранов и диафрагм часть главных дифракционных максимумов с помощью диафрагмы, помещенной в фокальную плоскость линзы. При таком перекрытии изображение решетки в плоскости Р¢Р¢ получается искаженным, так как оно соответствует решетке, у которой при дифракции эти максимумы не возникают. Когда диафрагма пропускает только один пучок от М ₀, достигающий плоскости Р¢Р¢, свет будет состоять только из одной волны, которой не с чем интерферировать. Изображение получается бесструктурным и представляет собой более или менее равномерно освещенное поле, какое наблюдалось бы, если бы на месте решетки РР находилась прозрачная плоскопараллельная пластинка. Когда диафрагма в плоскости FF открывает кроме главного максимума М ₀ еще максимумы первого порядка М ₁ и 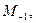исходящие из них волны интерферируют в плоскости Р¢Р¢. Возникает изображение решетки с плавным переходом от прозрачных к непрозрачным участкам. Точно такая же картина наблюдалась бы в случае, когда на месте щелевой решетки РР находилась бы решетка того же периода d, но с гармонической функцией пропускания. Действительно, при дифракции на такой решетке возникают главные максимумы только порядков m = 0, 1, т.е. 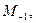максимумы М ₀, М ₁ и а это и имеет место в рассматриваемом случае. При увеличении числа открываемых максимумов изображение решетки будет все больше и больше становиться подобным самой решетке. Однако точное подобие достигнуто не будет, так как из-за конечных размеров линзы не все лучи, проходящие через максимумы, попадают в линзу и, кроме того, само число дифракционных максимумов, создаваемых решеткой, ограничено: m _max = целое число £ d / l.

Поскольку сходство изображения решетки с самой решеткой (когда в изображении решетки оказывается разрешенным основной период d решетки) появляется при m = 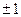, то наименьший период (размер) объекта, который может быть разрешен при заданной апертуре линзы 2 s_A, можно определить из условия откуда находим, что d = l / sin s_A.

Закроем все максимумы, кроме центрального максимума М ₀ и двух боковых максимумов М ₂ и Тогда опять получим случай гармонической решетки, с той лишь разницей, что максимумы 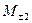будут более удалены друг от друга, чем максимумы . Если оставить открытыми только M ₀ и два максимума то период решетки, изображаемой в плоскости Р¢Р¢, станет еще меньше (в три раза) и т.д. Все происходит так, как если бы решетка-объект РР представляла собой суперпозицию бесконечного числа гармонических решеток с разными периодами d, d / 2, d / 3 и т.д. Математически это можно выразить, представив функцию пропускания щелевой решетки t (x) в виде ряда Фурье (п. 7.3.2):

t (x) = ,

где

A _m / 2 = ,

a – ширина щели. Каждый член этого ряда описывает одну гармоническую решетку. Каждая из таких решеток дает в плоскости FF две освещенные точки справа и слева от М ₀, соответствующие главным максимумам ±1-го порядка, полученным от этой решетки. Пары главных дифракционных максимумов порядка m обусловлены соответствующими парами гармоник (фурье-компонентами, т.е. членами ряда t_m (x) = 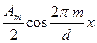) с амплитудами пространственными частотами m / d и пространственными периодами d / m. Член t ₀ = соответствует равномерному распределению света в плоскости решетки, и можно считать, что он принадлежит гармонической решетке с бесконечно большим периодом.

Все детали изображения решетки строятся способом, вполне аналогичным фурье-синтезу (сложению фурье-компонент). Но дифракционные максимумы сами заключают в себе разложение Фурье (фурье-синтез) решеточного объекта (точнее, его функции пропускания), а дифракционная плоскость описывается как фурье-плоскость. Поэтому процесс формирования изображения в рассматриваемом примере можно интерпретировать как двойное преобразование Фурье. Первое преобразование – это разложение светового излучения в фурье-спектр в фокальной плоскости линзы, т.е. образование фраунгоферовской дифракционной картины, а второе – суммирование этих фурье-компонент (фурье-синтез данного фурье-анализа) в плоскости изображения, т.е. образование собственно изображения. Такую интерпретацию легко понять, если воспользоваться принципом обратимости. Все порядки дифракции, которые создают изображение путем суммирования гармоник, возвращают к решеточному объекту, где они рекомбинируют (на второй стадии формирования изображения), образуя первоначальное распределение интенсивности на решетке.

Таким образом, согласно теории Аббе – Портера, изображение получается двумя последовательными этапами: дифракцией на предмете и образованием фраунгоферовой дифракционной картины в фокальной плоскости линзы и последующим преобразованием дифрагировавших пучков линзой в реальное оптическое изображение в сопряженной плоскости. Первому этапу соответствует фурье-анализ, а второму – фурье-синтез.

Представление о двойном преобразовании Фурье полностью согласуется с интерпретацией двойной дифракции Цернике. По существу это два различных способа выражения одного и того же явления.

Рассмотренный выше подход можно применить и к любым непериодическим структурам, так как дискретные порядки дифракции не являются его необходимыми условиями. В основе проведенного рассмотрения лежит тот факт, что изображение в плоскости P¢P¢ решеточного объекта, расположенного в плоскости PP, формируется только световыми пучками, проходящими через плоскость FF, т.е. пучками, образующими дифракционные спектры. Непериодический объект можно рассматривать как одну щель решетки, но не с прямоугольной, а с произвольной функцией пропускания t (x, y). Как и в случае щели, функция пропускания такого объекта может быть представлена не рядом, а интегралом Фурье. Дифракционная картина в фокальной плоскости линзы (дифракционной плоскости) в этом случае будет представлять собой картину непрерывного рассеяния волн с угловым изменением амплитуды и фазы, зависящим от функции пропускания объекта. При этом крупные детали объекта, которым соответствуют низкие пространственные частоты, дают дифрагировавшие лучи, которые мало отклоняются от направления прямого пучка. Мелкие детали, которым соответствуют высокие частоты, дают дифрагировавшие лучи, сильно отклоненные от прямого пучка. Эта картина является двумерным преобразованием Фурье от функции распределения комплексной амплитуды поля по объекту E (x, y). Восстановление этой картины в плоскости изображения сводится к суммированию интерференционных полос, создаваемых парами дифрагировавших лучей (под углами на рис 11.5), но с произвольным расстоянием между полосами и их ориентацией.

Формирование изображения и в случае непериодических объектов можно описать как процесс двойного преобразования Фурье. При освещении транспаранта параллельным пучком монохроматического света проходящая через транспарант плоская монохроматическая волна дифрагирует на неоднородностях прозрачности изображенного на транспаранте предмета (модулируется по амплитуде и фазе в плоскости предмета) так, что в плоскости XY непосредственно за транспарантом возникает распределение комплексной амплитуды E (x, y) = E ₀ t (x, y), где E ₀ – амплитуда падающей на транспарант плоской волны, t (x, y) – функция пропускания транспаранта. Поле световой волны в плоскости XY можно разложить в двумерный интеграл Фурье, т.е. представить в виде совокупности бесконечного числа плоских дифрагировавших волн с пространственными частотами u и v и соответствующими амплитудами и фазами. Комплексная амплитуда дифрагировавшей волны с волновым вектором k (2 pu, 2 pv) пропорциональна соответствующей фурье-компоненте (пространственной гармонике) E (u, v) функции E (x, y) предмета:

E (u, v) = . (11.26)

Каждый пучок параллельных лучей, получившийся в результате дифракции на транспаранте, собирается линзой в соответствующей точке фокальной плоскости. Возникает дифракционная картина, в которой, как было показано в п. 10.5, распределение амплитуды поля E_f (x_f, y_f) представляет собой двумерный фурье-образ E (u, v) функции E (x, y) предмета.

Проходящие через расположенные в фокальной плоскости линзы точки максимумов дифрагировавшие волны в плоскости Р¢Р¢ изображения интерферируют между собой. В линзе с исправленными аберрациями оптические пути между всеми парами сопряженных точек одинаковы, поэтому при интерференции волны в точках (x¢, y¢) плоскости Р¢Р¢ их сложение происходит с теми же относительными фазами, которые они имели в соответствующих точках (x, y) плоскости РР предмета. Распределение амплитуды светового поля в плоскости изображения Р¢Р¢, будет описываться (с точностью до масштаба) таким же интегралом Фурье, что и в плоскости РР предмета:

E¢ (x¢, y¢) = 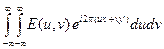. (11.27)

Отметим, что первое преобразование Фурье (прямое) описывает первую дифракцию – дифракцию на апертуре линзы, а второе (обратное) – вторую дифракцию, которая осуществляется в результате распространения света в свободном пространстве между задней фокальной плоскостью линзы и плоскостью изображения.

Хотя пределы интегрирования по u и v, т.е. по направлениям дифрагировавших волн (так как каждому значению u и v соответствует вполне определенное направление распространения дифрагировавшей волны), в интеграле (11.27) указаны равными , на самом деле интегрирование производится в пределах, определенных апертурой линзы.

В плоскости изображения Р¢Р¢ в результате интерференции дифрагировавших волн возникает распределение светового поля, воспроизводящее (в измененном масштабе) распределение поля E (x, y) в плоскости РР предмета. Однако это воспроизведение не будет точным, поэтому восстановленное изображение не будет полностью идентично изображению предмета на транспаранте. Хотя распределение амплитуды светового поля в плоскости изображения описывается (с точностью до масштаба) тем же интегралом Фурье (11.27), что и в плоскости предмета, но в этот интеграл входят не все фурье-компоненты E (u, v) функции предмета E (x, y), а только те, которым соответствуют прошедшие через линзу дифрагировавшие волны. Угол дифракционной расходимости j дифрагировавшего пучка определяется соотношением sin j ~ l / a, где a – линейный размер объекта. Поэтому если объект очень мал (а ≈ l), то дифрагировавшие на нем волны будут идти под большим углом к оптической оси и могут не попасть в линзу. По этой причине пространственные гармоники E (u, v), соответствующие мелким деталям предмета, будут отсутствовать в формируемом линзой изображении, если соответствующие им дифрагировавшие волны имеют угол дифракции j > s_A, где 2 s_A – апертура линзы. Это и приводит к тому, что распределение амплитуды светового поля в плоскости изображения не дает точного воспроизведения функции E (x, y) предмета. Линза из-за конечных размеров апертуры не способна отобразить объект, размеры которого соизмеримы с длиной волны света. Вследствие этого и происходит потеря точности восстановления изображения.

Аналогично и в случае решеточного объекта. Изображение решетки получилось бы полностью подобным самой решетке со всеми ее деталями, если бы распределение света в плоскости изображения Р¢Р¢ представлялось бы рядом Фурье с теми же коэффициентами, что и в плоскости предмета. Однако это оказывается невозможным. Из ряда Фурье выпадают компоненты, соответствующие волнам, которые не попадают в линзу из-за конечных размеров ее апертуры. Изображение соответствует суперпозиции только тех гармонических решеток, главные дифракционные максимумы которых вошли в оптическую систему.

Проиллюстрируем представление о двойной дифракции на примере когерентно освещенного одномерного периодического решеточного объекта с гармонической функцией пропускания

t (x) =

где d – период решетки. Распределение амплитуды поля по объекту

E (x) = E ₀ t (x) = E ₀

где E ₀ – амплитуда плоской волны, падающей на объект. При первой дифракции в фокальной плоскости линзы образуется дифракционная картина (спектр)

E (u) =

= +

+ = E ₀ [ d (u) + d (u – 1/ d) +

+ d (u + 1/ d)]. (11.28)

При получении этого выражения поле E (x) было представлено в виде

E (x) = E ₀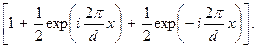

В данном случае дифракционная картина состоит из трех разделенных плоских волн, которые условно изображаются тремя пиками на спектре – спектральными линиями. Фурье-координаты этих пиков u = 0, ± 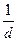. Декартовы координаты этих пиков в фокальной плоскости линзы определяются значениями (11.28). Если эти спектральные линии попадают в апертуру линзы, то, согласно представлению о двойной дифракции, поле в плоскости изображения (с точностью до масштаба) будет

E¢ (x¢) = =

= +

+ =

= E ₀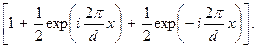

Это выражение показывает, что амплитуда изображения имеет ту же периодичность, что и амплитуда предмета. С точностью до масштаба изображение объекта оказывается полностью идентичным самому объекту.

Найдем максимальное значение пространственной частоты, пропускаемой линзой. Представим себе, что функция пропускания 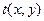объекта разложена на фурье-компоненты, описывающие пропускание гармонических решеток. Рассматривая распространение световых волн в плоскости XZ, возьмем одну из фурье-компонент (одну гармоническую решетку), составляющих пропускание 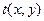, с пространственной частотой u. Если плоская волна падает на решетку неограниченных размеров, то дифрагировавшие волны будут плоскими, а углы дифракции будут определяться формулой sin j = ± l / d = ± l u. Если пренебречь дифракцией на краях транспаранта (решетки), то можно считать, что любой малый пучок лучей, падающий на произвольно малый участок решетки, дифрагирует под углом 𝜑. Рассмотрим для простоты пучок лучей с вершиной, расположенной на оси Z. Максимальный угол, под которым эти лучи могут дифрагировать, попадая при этом в линзу радиусом R, определяется отношением tg j = = R / a, где a – расстояние от транспаранта до линзы. Будем считать, что угол дифракции j мал, так что R / a = tg j ≈ sin j. Тогда для центральных лучей получим, что максимальная пространственная частота u ₀ входной решетки, которую линза может преобразовать в изображение, определяется соотношением

sin j = lu ₀ £ R / d,

т.е. не превосходит величины

u ₀ = R / la. (11.29)

Таким образом, линза конечного радиуса R преобразует в изображение всю световую информацию о предмете, которую несут компоненты с пространственными частотами вплоть до частоты u ₀. Если пространственная частота какой-либо компоненты пропускания превышает значение u ₀, то соответствующая ей информация теряется.

Мы видим, что оптическое изображение можно рассматривать как передачу информации. Отображаемый предмет осуществляет пространственную модуляцию световой волны, вызывая появление дифрагировавших волн. Эти отклоненные на разные углы волны несут информацию о структуре предмета. При этом информация о структуре предмета в получаемом изображении будет полной, если все дифрагировавшие волны проходят через линзу и участвуют в создании дифракционной картины на экране (участвуют в формировании изображения) и неполной – если какие-либо волны не попадут в линзу. Чем больше дифрагировавших волн различных порядков проходит через линзу, тем совершеннее получается изображение, тем, следовательно, больше информации о структуре предмета оно несет.

Теория формирования изображения Аббе – Портера послужила основой создания метода фильтрации пространственных гармоник, который применяется при оптической обработке. Эта теория сыграла важную роль в разработке теоретических основ фазового контраста и его разновидностей. Метод фазового контраста применяется в микроскопии и в настоящее время. Теория Аббе – Портера сыграла роль и при создании нового метода получения высококачественного изображения, называемого голографией. Все эти вопросы будут рассмотрены нами в 12 и 13 главах.

[1] Отверстие можно рассматривать как транспарант, функция пропускания которого принимает только два значения: единица в отверстии и нуль – вне пределов отверстия.

[2] Подробно об этом будет говориться в п. 10.6.

[3] Об этом будет подробно говориться в следующей главе.

Не нашли, что искали? Воспользуйтесь поиском: