Параграф 2. Подпространства

Пусть дано ЛВП V

Непустое множество v’ называется подпространством ЛВП V если выполнены условия:

1) Сумма любых двух векторов из множества v’ также является вектором этого множества

2) Произведение любого вектора V’ на скаляр(число) так же является вектором данного множества V’

Ядро гомоморфизма

Пусть дан гомоморфизм

Ядром гомоморфизма f называется множество всех таких векторов из ЛВП V, образом которых является нулевой вектор ЛВП W.

Образ гомоморфизма

Образом гомоморфизма f называется множество все нетривиальных векторов ЛВП W являющихся образами ненулевых векторов из ЛВП V:

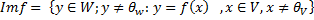
Теорема о ядре и образе гомоморфизма:

Пусть гомоморфизм между ЛВП V и W

Ядро гомоморфизма f является подпространством ЛВП V

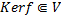
Образ гомоморфизма f является подпространством ЛВП W.

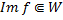
Доказательство:

1) Покажем что ядро гомоморфизма f является подпространство ЛВП V.

- Выберем 2 элемента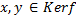

- Проверим выполняются ли понятие подпространства и основные свойства понятия гомоморфизма:

(1)

Из равенства (1) видно, что сумма двух векторов из ядра имеет образ нуль –вектора ЛВП W. Это означает что сумма двух векторов принадлежит ядру гомоморфизма (Первое условие определения подпространства.)

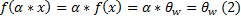
Из неравенства (2) следует, что произведение произвольного скаляра на произвольный вектор x из ядра, так же является вектором из ядра (второе условие определения подпространства)

2) Покажем, что образ гомоморфизма f является подпространством ЛВП W

- Выберем x’ и y’ из образа f

- Проверим выполняется ли понятие подпространства и основные свойства понятия гомоморфизма.

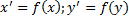
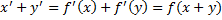
Так как сумма векторов x’ и y’ не является нуль-вектором и согласно определению ядра, эта сумма является образом сумы двух ненулевых векторов из ЛВП V.

Доказательство второго свойства гомоморфизма основываются на приведенных выше выкладках.

Теорема о простейших свойствах гомоморфизмов:

Пусть . Имеет место следующие простейшие свойства

1)

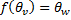
2)

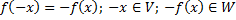
Теорема о простейших свойствах изомофризма:

Пусть 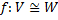. Имеют место следующие простейшие свойства:

1) Образом любого ненулевого вектора из V является ненулевой вектор из W

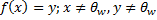
2)

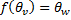
3) Образами векторов, образующих линейно независимую систему в ЛВП V, являются векторами их ЛВП W, которые так же образуют линейно независимую систему.

, такие ЛНВС ЛВП W/

4) Пусть дана произвольная линейно зависимая система векторов из ЛВП V, причем их линейная комбинация (не тривиальная), приравнена к 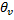, с некоторыми скалярами тогда образом этой системы будет являтся так же линейно зависимая система векторов. При чем нетривиальная линейная комбинация образов приравненная к 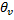с теи же скалярами

Не нашли, что искали? Воспользуйтесь поиском: