Параграф 3. Корни многочленов.

Пусть дано

Зафиксируем произвольны мобразом некоторое значение переменой х, х=с (с- константа). Подставить это значение в (1), получим число которое называется значением полинома f в точке x=c.

Значения полинома в некоторой точке обладают следующими свойствами:

1)

2)

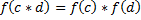
3)

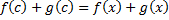
4)

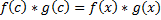
Число «c» называется корнем полинома f, если значение f(с) равно нулю.

Число С называется корнем кратности K, если многочлен f можно представить в виде:

Если к=1, то корень называется простым.

Задача отыскания корней многочлена связана с задачей разложения многочлена f на линейные множители kx+b/

Теорема Безу:

Остаток от деления полинома f ненулевой степени на моном (x-c) равен f(c).

Следствие из теоремы Безу:

Если остаток от деления полинома f на моном (x-c) равен нулю, то c является корнем полинома f

Схема Горнера:

Не нашли, что искали? Воспользуйтесь поиском: