Параграф 4. Аффинные подпространства и r-мерные плоскости в аффинном пространстве.

Пусть дано ЛВП размерности n(dimV=n)

Рассмотрим произвольную систему линейных однородных уравнений от n переменных. Пусть ее ранг равен r.

Теорема (о подпространствах порожденных слоу): Совокупность всех решений СЛОУ образует линейное векторное подпространство размерностью n-r в ЛВП порожденного фундаментальной системой решений СЛОУ

Аффинные пространства:

В классическом определении ЛВП можно считать, что его элементами являются n-мерные точки. Расширим понятие ЛВП, добавив к его элементам понятие геометрического вектора, тем самым получим понятие точечно-векторного или аффинного пространства.

Пусть имеется ЛВП, элементами которого являются точки. Каждым любым двум точкам этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором(вектором).

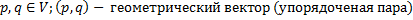
Точки и вектора в получившемся аффинном пространстве обладают следующими свойствами (аксиомы аффинного пространства):

1) Для каждой точки М и каждого вектора х существует точка N такая, что

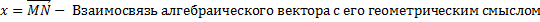
2) Для любых точек M,N и P выполнимо равенство:

3) Совокупность всех точек ЛВП пополненная векторами, удовлетворяющих аксиомам, называют точечно- векторным или аффинным пространством. Аффинное пространство является n-мерным, если соответствующие ЛВП так же являются n- мерными.

Предложение(О простейших свойствах векторов аффинного пространства):

1) Если 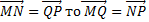. Данное свойство непосредственно следует из равенства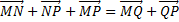

2) Вектор, у которого начало и конец совпадают, являются нулевым вектором n- мерного аффинного пространства.

Это следует из равенства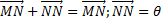

3) Для каждого вектора существует противоположный у нему вектор.

Это следует из равенства: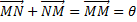

Пусть задана т. О (начало координат) и система базисных векторов приложенных к точке О.

Согласно понятию ЛВП вектор х есть 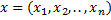. То по аксиоме 1.АП (Аффинных пространств) имеет место следующее OX=X и . Координатами вектора в АП считают координаты соответствующего алгебраического вектора

В случае когда заданы произвольные 2 точки. 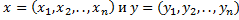, то

Действительно, рассмотрим равенство:

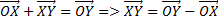
Что и требовалось доказать.

Теорема о изоморфизме аффинных пространств:

Естественным образом возникает вопрос, будут ли изоморфными 2 аффинных пространства в случае когда изоморфными являются соответствующие лвп.

Утвердительный ответ дается в Теореме (об изоморфизме аффинных пространств):

Любые два изоморфных аффинных пространства имеют одинаковую размерность (т.е они изоморфны только в этом случае)

Доказательство:

A и A’ называют изоморфными, если существует взаимно-однозначное отображение такое, что выполнены свойства:

1)

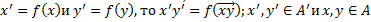
Остальные свойства те же, что и свойства в определении изоморфизма ЛВП.

Выберем в каждом из А и А’ две точки такие, что координаты их будут равны, тогда имеет место следующее:

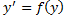
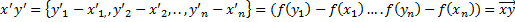
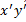является образом при изоморфизме, что можно установить, пользуясь понятием изоморфизма между ЛВП и его простейшими свойствами.(все тоже самое что и выше, только в обратном порядке)

Переход от базиса к базису в аффинном пространстве:

Случай 1: Переход от базиса к базису имеющих общую точку приложения:

В данном случае переход осуществляется с помощью матрицы перехода, составленной из координат нового базиса. Преобразование координат вектора при таком переходе осуществляется с помощью известных алгебраических действий.

Случай 2: Переход от базиса к базису с изменением точки приложения базисных векторов.

Дальнейшие рассуждения базируются на равенстве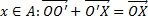

Координаты вектора при переходе от старого базиса к новому изменяются в соответствии с известными алгебраическими действиями с учетом вычитания вектора соединяющего точки приложения базисного векторов.

Не нашли, что искали? Воспользуйтесь поиском: