Параграф 2. О делимости многочленов

Пусть даны 2 полинома f и g, degf>=degg

Полином f делится нацело на полином g, если существует такой полином h, что выполняется равенство f=g*h.

Замечание: Причем полином h, в силу теоремы о делении с остатком, является единственным.

Полином g Называется делителем полинома f. При использовании теоремы о делении с остатком возможна ситуация, когда коэффициенты полинома f рациональны или действительны, то может оказаться, что коэффициенты полинома h не будут таковыми. Они будут комплексными, то есть все равно их можно будет считать рациональными или действительными.

Приведем ряд основных свойств делимости полиномов:

1) Свойство транзитивности деления:

Если полином f Делится на полином g, а полином g Делится на полином h, то f Делится на h

2) Если полиномы f и g делятся на полином h, то их сумма(разность) так же делится на h.

3) Если полином f делится на полином g, то и произведение полинома f на любой другой также будет делиться на полином g.

4) Обобщение свойств 2 и 3

Если каждый полином из конечного набора полиномов делится на полином g то и линейная комбинация (сумма произведений) полиномов из набора с другими так же будет делиться на полином g.

5) Любой произвольны полином всегда делится на полином нулевой степени (на число)

6) Если полином f делится на полином g. То так же он делится и на полином c*g (с – скаляр)

7) Все делители полинома f так же будут делителями полинома c*f.

8) Полиномы f и g делятся друг на друга, если имеют пропорциональность на число между многочленами.

Примечание: в свойствах речь идет о ненулевых делителях.

Путь даны 2 полинома f и g. Полином h называется общим делителем полиномов f и g, если он делит полиномы f и g и делит любой другой делитель полиномов f и G. Если найдутся такие, которые не делят полином h на цело, то тогда среди них можно найти общий делитель полиномов f и g.

Полином h называется НОД, если он будет делиться на любой другой делитель полиномов f и g (имеет наибольшую степень)

H=НОД(f,g)

Для нахождения НОДа двух полиномов используют алгоритм Евклида.

Алгоритм Евклида:

1)

2)

3)

4) …………………….

n)

n+1)

Алгоритм прерывается. Тот остаток r(n), который нацело делит предыдущий остаток r(n-1) будет НОДом f и g

Теорема о представлении НОДа:

1) Если многочлен a (альфа) является НОДом f и g, то имеет место равенство

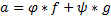, где полиномы определяются однозначно.

2) Если многочлены f и g являются взаимно простыми, то имеет место равенство:

, где полиномы определяются однозначно.

Два полинома f и g называются взаимно простыми, если их наибольший общий делитель равен произвольному полиному нулевой степени. Согласно свойствам делимости, этот полином можно считать равным единице.

Доказательство на частном случае двух полиномов третей и второй степени, используя обратный ход алгоритма Евклида. (сами)

Набросок доказательства к теореме о представлении НОД:

Рассмотрим k-1 шаг в алгоритме Евклида:

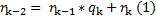
Так как (При условии что последний шаг дает деление на ноль) перепишем равенство (1) в виде:

В равенстве (2) получим: 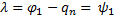, тогда

Из шага к-3 выразим r(k-1) через r(k-2) и r(k-3)

Подставляем в равенство (3):

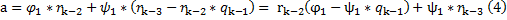
В (4) введем переобозначение: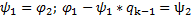

И получим: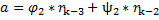

Далее действуем аналогично, выражая из предыдущего шага, приводя подобные и вводя переобозначения. Так до первого шага, где в итоге получаем требуемую формулу:

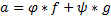
Теорема о простейших свойствах взаимно простых полиномов:

1) Если многочлен F является взаимно простым с многочленом g и h, то он так же будет взаимно простым с g*h

2) Если произведение g*h делится на многочлен f, причем f и g являются взаимно простыми, то тогда многочлен h делится на многочлен f.

3) Если многочлен f Делится на многочлены g и h, которые между собой взаимно простые, то он делится и на произведение g *h

Теорема о НОДе конечной системы полиномов:

Пусть дана конечная система полиномов f0,f1,..,fk+1, тогда НОД этой системы равен наибольшему общему делителю многочлена fk+1 и НОДа многочленов f0,f1,…,fk.

Не нашли, что искали? Воспользуйтесь поиском: