Пересечение и сумма подпространств ЛВП.

Пусть даны подпространства v’’ и v’.

Пересечение подпространств v’ и v’’ называется множество векторов принадлежащих одновременно и v’ и v’’

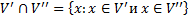
Теорема о пересечении подпространств:

Пересечение любых двух подпространств ЛВП является подпространством исходного ЛВП.

Доказательство: Самостоятельно детишки)

Примечание к теореме:

Не всегда имеет место тот факт, что объединение двух подпространств ЛВП являются подпространством исходного ЛВП.

Суммой двух подпространств v’ и v’’ называется множество всевозможных линейных комбинаций из двух векторов принадлежащих соответственно v’ и v’’

Теорема о сумме подпространств:

Сумма любых двух подпространств ЛВП является подпространством исходного ЛВП.

Доказательство: И тут снова самостоятельно)

Размерностью Подпространства, как и самого пространства называется число базисных векторов соответственно.

Обозначение: dimV

Теорема о размерности ЛВП:

Размерность пространства равна сумме размерностей заданных подпространств за исключением размерностей пересечений подпространств, составляющих собой исходное ЛВП.

Прямой суммой двух подпространств v’ и v’’ называется обычная сумма при условии что эти подпространства не пересекаются

Теорема о прямой сумме:

Размерность ЛВП равна сумме размерностей непересекающихся подпространств

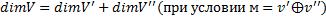
Теорема о размерности ядра и образа гомоморфизма:

- гомоморфизм

Если dimV=n; dim(kerf)=r, То dim(Imf)=n-r

Доказательство:

Пусть размерность V (dimV) равна n и – это базис гомоморфизма (kerf)

И – дополнение до базиса пространства V.

Предположим что векторы при гомоморфизме f образуют базис его образа

Получим: ,..,

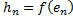
Предположим противное, то есть образуют линейно зависимую систему. Согласно понятию линейной зависимости существует нетривиальная линейная комбинация такая, что

Далее, пользуясь понятием гомоморфизма, получаем следующее:

НО! Полученный результат противоречит тому факту, что векторы являются дополнением до базиса ЛВП V. Это означает что векторы 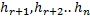образуют линейно независимую систему (исключаем второе предположение), то есть эта система является кандидатом на роль базиса в ЛВП W.

Покажем, что это действительно так.

Воспользуемся свойствами гомоморфизма и понятием ядра

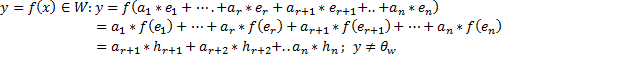
Из вышеприведенных рассуждений видно, что произвольный ненулевой вектор y из ЛВП W(представим) разложим по базису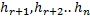

Не нашли, что искали? Воспользуйтесь поиском: