Параграф 2. Комплексные числа в тригонометрической форме

Пусть дано число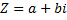

(Тут какой то рисунок в лекции..я перерисовывать его не буду)

(Ребят, в ворде «альфа» не отличается почти от «а». не перепутайте! В аргументе у косинуса и синуса стоит «Альфа», а в самих формулах «а»)

Угол наклона комплексного числа к оси действительных частей называется аргументом комплексного числа.

(Тут опять же «альфа»)

Теорема (об операциях над комплексными числами в тригонометрической форме):

Пусть даны:

1)

2)

3)

При делении комплексных чисел аргументы вычитаются, а при умножении складываются.

4)

5) Возведение комплексного числа в степень (формула Муавра)

6) Общая формула Муавра

Комплексные числа в форме Эйлера.

Операции над комплексными числами в форме Эйлера:

1)

2)

3)

4)

5)

6)

Группа корней n-ой степени из единицы:

Комплексные числа разбивают единичную окружность на равные части. Получаем правильный многоугольник.

При сложении и умножении чисел всегда получаются числа из этой же группы. Любое комплексное число можно выразить через

Глава 6.

Кольцо полиномов К

Не нашли, что искали? Воспользуйтесь поиском: