Задача 7. Вычислить определенный интеграл с симметричными пределами

7.1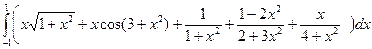

7.2 ;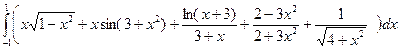

7.3 ;

7.4 ;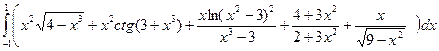

7.5 ;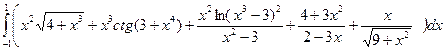

7.6 ;

7.7 ;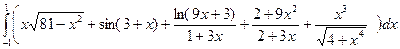

7.8 ;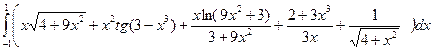

7.9 ;

7.10 .

Пример решения Задачи 7. Вычислим определенный интеграл

;

Искомый интеграл равен сумме пяти интегралов:

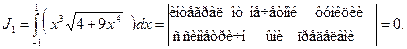
0.

0.

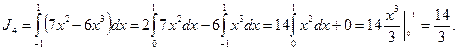
Здесь первый интеграл берется от четной функции с симметричными пределами, а второй - от нечетной.

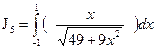= 0.

Задача 8. Участок земли ограничен изображенными на рисунке кривыми. Считая кривые вертикальной и горизонтальной параболами, найти площадь участка, если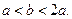

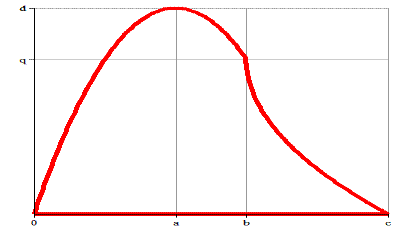
1. a=300 м; d=400 м; b=400 м; c=600 м.

2. a=200 м; d=300 м; b=400 м; c=1000 м.

3. a=100 м; d=150 м; b=150 м; c=300 м.

4. a=250 м; d=200 м; b=400 м; c=600 м.

5. a=300 м; d=200 м; b=500 м; c=500 м.

6. a=400 м; d=300 м; b=600 м; c=900 м.

7. a=250 м; d=400 м; b=400 м; c=700 м.

8. a=350 м; d=300 м; b=600 м; c=600 м.

9. a=200 м; d=400 м; b=300 м; c=600 м.

10. a=100 м; d=200 м; b=170 м; c=400 м.

Пример решения Задачи 8. Пусть значениями параметров являются следующиевеличины

a=100 м; d=100 м; b=150 м; c=250 м.

Тогда уравнения парабол можно представить в виде:

левая вертикальная парабола

правая горизонтальная парабола 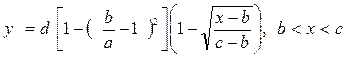, 0 < x < b.

Значение параметра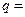

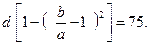
Искомая площадь S участка выражается с помощью определенного интеграла в виде

участка выражается с помощью определенного интеграла в виде

S=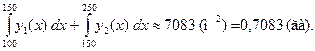

Не нашли, что искали? Воспользуйтесь поиском: