УРАВНЕНИЕ НАВЬЕ-СТОКСА

ВЯЗКАЯ ЖИДКОСТЬ

В этом разделе изучим основные закономерности движения вязкой жидкости. Ограничимся рассмотрением лишь ньютоновских жидкостей, для которых модуль сдвига равен нулю, т.е. .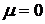

УРАВНЕНИЕ НАВЬЕ-СТОКСА

В разделе 1 (п.6.4.) было получено уравнение сохранения количества движения (импульса единицы массы) - уравнение движения в фундаментальной системе уравнений сохранения (6.9.1). Это уравнение содержит производную по координатам тензора упругих напряжений . В случае, если в среде имеют место и неупругие напряжения, описываемые тензором неупругих (вязких) напряжений , то в уравнении движения (6.9.1) вместо тензора 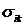должен быть подставлен полный тензор напряжений , определяемый согласно (6.11.1). Тогда уравнение движения (6.9.1) принимает форму:

(8.1.1)

Для ньютоновских жидкостей (), испытывающих только всестороннее сжатие или растяжение, полный тензор напряжений в изотермических условиях согласно (5.2.5а) и (6.10.4) равен:

. (8.1.2)

После вычисления производной , подстановки её в (8.1.1) и приведения подобных, уравнение движения для 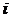- ой компоненты скорости индивидуальной частицы принимает вид:

(8.1.3)

Если вместо коэффициента динамической вязкости 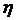ввести коэффициент кинематической вязкости , то уравнение движения можно записать в векторной форме:

(8.1.4)

Уравнения (8.1.3) и (8.1.4) называются уравнениями Навье-Стокса для вязкой жидкости. Для несжимаемой жидкости 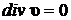и уравнение Навье-Стокса записывается в виде:

(8.1.5)

Из уравнений (8.1.3) и (8.1.4) видно, что уравнение Навье-Стокса отличается от уравнения Эйлера (7.1.2) дополнительными слагаемыми в правой части, учитывающими вязкость жидкости.

Замкнутая система уравнений сохранения массы, импульса и внутренней энергии вязкой жидкости включает также уравнение непрерывности движения (6.3.5) и уравнение сохранения внутренней энергии (6.7.10) с заменой в нем 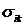на , т.е.

(8.1.6)

Уравнения (8.1.5), (8.1.6) вместе с термическим и калорическим уравнениями состояния и законом Фурье () образуют замкнутую систему уравнений движения вязкой жидкости. Предполагается, что решение этой системы существует и при заданных начальных и граничных условиях оно единственно.

Не нашли, что искали? Воспользуйтесь поиском: