Распределение скорости в поле течения около шара

Используя определение скорости движения частиц жидкости, имеем:

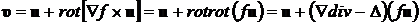. (8.4.15)

Поскольку 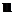- постоянный вектор, то, используя (8.4.14), третье слагаемое в (8.4.15) преобразуем к виду:

.

Аналогично преобразуем второе слагаемое в (8.4.15):

После подстановки полученных выражений в (8.4.15) и группировки соответствующих слагаемых вектор скорости потока в точке r поля течения равен:

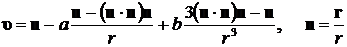. (8.4.16)

Постоянные a и b должны быть определены из граничных условий на поверхности шара: при

Так как вектор скорости жидкости должен быть равен нулю в любой точке на поверхности шара, т. е. при любой ориентации единичного нормального вектора , то, следовательно, должны обращаться в нуль в отдельности коэффициенты при векторах 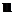и в выражении (8.4.16):

1. при u: 2. при (u ∙ n) n:

Решение этой системы уравнений приводит к результату:

. (8.4.17)

Очевидно, что картина обтекания шара (рис. 8.10) имеет сферическую симметрию, поэтому . Компоненты скорости и могут быть найдены из (8.4.16) и (8.4.17) в виде:

Таким образом, компоненты и скорости движения индивидуальной частицу при медленном обтекания шара потоком вязкой несжимаемой жидкости определяются соотношениями:

(8.4.18)

На поверхности шара в любой точке , а, следовательно, и в соответствии с граничными условиями.

Не нашли, что искали? Воспользуйтесь поиском: