
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные затруднения при решении уравнения Навье-Стокса
Уравнение Навье-Стокса (8.1.5) по сравнению с уравнением Эйлера содержит наряду с первыми и вторые производные скорости по координатам. Основная трудность решения уравнения движения вязкой жидкости заключается в нелинейности уравнений, обусловленной слагаемым 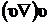 , а не в дополнительных слагаемых, учитывающих вязкие силы. В теории движения идеальной жидкости эту трудность обходили, полагая движение потенциальным, т. е. предполагали
, а не в дополнительных слагаемых, учитывающих вязкие силы. В теории движения идеальной жидкости эту трудность обходили, полагая движение потенциальным, т. е. предполагали 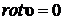 . Если для идеальной жидкости предположение о потенциальности движения не противоречило механической модели жидкости, то движение вязкой жидкости в общем случае не является потенциальным. Можно назвать лишь несколько частных случаев, когда движение вязкой жидкости потенциально. Так, например, в предыдущем разделе было показано (п. 7.4.3), что движение в любой точке, кроме оси плоского вихря постоянной интенсивности, является потенциальным вне зависимости от модели жидкости. Поэтому существует очень мало точных решений уравнения Навье-Стокса. Эти точные решения могут быть получены в том случае, когда удается тем или иным способом избавиться от нелинейного слагаемого
. Если для идеальной жидкости предположение о потенциальности движения не противоречило механической модели жидкости, то движение вязкой жидкости в общем случае не является потенциальным. Можно назвать лишь несколько частных случаев, когда движение вязкой жидкости потенциально. Так, например, в предыдущем разделе было показано (п. 7.4.3), что движение в любой точке, кроме оси плоского вихря постоянной интенсивности, является потенциальным вне зависимости от модели жидкости. Поэтому существует очень мало точных решений уравнения Навье-Стокса. Эти точные решения могут быть получены в том случае, когда удается тем или иным способом избавиться от нелинейного слагаемого 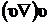 .
.
В чисто математическом смысле краевые задачи теоретической гидродинамики чрезвычайно трудны. Поэтому становление теории шло бы гораздо медленнее, если бы строгая математика не дополнялась различными правдоподобными интуитивными гипотезами. Известный немецкий математик Биркгоф, анализируя в начале прошлого века положение в теоретической гидродинамике, назвал семь таких гипотез. Рассмотрим только две, которые понадобятся в дальнейшем:
1. При определении физических переменных в задачах можно полагаться на интуицию, которая может быть подкреплена оценкой слагаемых в рассматриваемых уравнениях.
2. Топологию течения, т.е. общее представление о поле течения жидкости, можно определить интуитивно, полагая, в частности, что симметричное воздействие вызывает симметричный эффект.
Конечно, с точки зрения чистой математики такие гипотезы не имеют права на существование в строгой теории. Но, как видно будет далее, они позволяют либо получить решение, либо значительно упрощают решение и приводят к результатам, хорошо согласующимися с опытными данными, что и является конечной целью всякого исследования.
Таким образом, решения, полученные на основании таких гипотез, необходимо проверять экспериментально. В случае адекватности предполагаемого на основании гипотез движения действительному, наблюдаемому в опыте, полученные решения можно считать точными.
Течение Куэтта
|
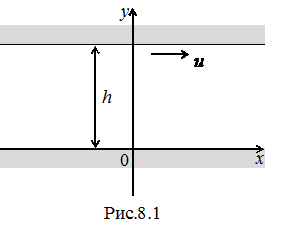
Рассмотрим вязкую несжимаемую жидкость, расположенную между двумя параллельными бесконечными плоскостями, находящимися на расстоянии 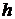 друг от друга. Пусть в некоторый момент времени верхняя плоскость (рис. 8.1) начинает двигаться и движется в дальнейшем с постоянной скоростью
друг от друга. Пусть в некоторый момент времени верхняя плоскость (рис. 8.1) начинает двигаться и движется в дальнейшем с постоянной скоростью  , параллельной нижней плоскости. Через некоторое время из-за прилипания жидкости к поверхностям между плоскостями установиться некоторое стационарное движение вязкой жидкости с некоторым распределением скорости вдоль оси у. Определим это установившееся распределение скорости.
, параллельной нижней плоскости. Через некоторое время из-за прилипания жидкости к поверхностям между плоскостями установиться некоторое стационарное движение вязкой жидкости с некоторым распределением скорости вдоль оси у. Определим это установившееся распределение скорости.
Так как плоскости в направлении оси 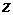 неограниченны, то можно рассматривать движение как плоское. Если ускорение силы тяжести направлено по оси y, а расстояние между плоскостями
неограниченны, то можно рассматривать движение как плоское. Если ускорение силы тяжести направлено по оси y, а расстояние между плоскостями 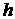 невелико, то можно пренебречь влиянием силы тяжести на движение жидкости в зазоре. Здесь использована гипотеза 1. Далее интуитивно полагаем, что скорость частиц жидкости в любой точке зазора направлена только вдоль оси x и зависит только от координаты y в силу бесконечности пластин в направлении x. Здесь использована вторая гипотеза об интуитивном определении топологии течения, основанная на предположении о симметрии эффекта при симметричном воздействии. Так как воздействие (движущаяся верхняя плоскость) симметрично относительно оси y, то и эффект (движение частиц жидкости) также будет симметричным относительно оси y, т. е. скорости частиц будут направлены только вдоль оси x. Движение жидкости будем полагать изотермическим. Таким образом, в этом случае нет необходимости рассматривать уравнение сохранения внутренней энергии. Необходимо решить уравнения при следующих условиях:
невелико, то можно пренебречь влиянием силы тяжести на движение жидкости в зазоре. Здесь использована гипотеза 1. Далее интуитивно полагаем, что скорость частиц жидкости в любой точке зазора направлена только вдоль оси x и зависит только от координаты y в силу бесконечности пластин в направлении x. Здесь использована вторая гипотеза об интуитивном определении топологии течения, основанная на предположении о симметрии эффекта при симметричном воздействии. Так как воздействие (движущаяся верхняя плоскость) симметрично относительно оси y, то и эффект (движение частиц жидкости) также будет симметричным относительно оси y, т. е. скорости частиц будут направлены только вдоль оси x. Движение жидкости будем полагать изотермическим. Таким образом, в этом случае нет необходимости рассматривать уравнение сохранения внутренней энергии. Необходимо решить уравнения при следующих условиях:
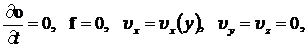 (8.3.1)
(8.3.1)
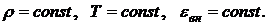
Запишем уравнение движения (8.1.5) для компонент скорости движения в декартовой системе координат и уравнение непрерывности (8.1.5) в форме:
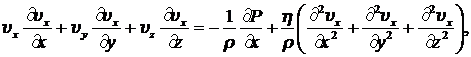
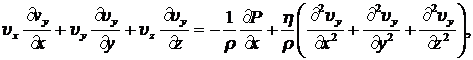 (8.3.2)
(8.3.2)
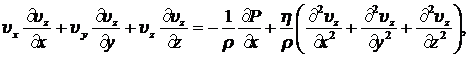

Из системы уравнений (8.3.2) видно, что при заданной топологии движения нелинейное слагаемое 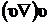 из уравнений исчезает. Так будет всегда, когда линии тока рассматриваемого движения параллельны.
из уравнений исчезает. Так будет всегда, когда линии тока рассматриваемого движения параллельны.
Используя условия (8.3.1), полученные интуитивно, из уравнений (8.3.2) получим следующие уравнения:
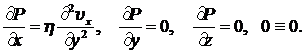 (8.3.3)
(8.3.3)
Из (8.3.3) видно, что при заданной топологии движения жидкости уравнение непрерывности удовлетворяется тождественно. Из 2-го и 3-го уравнений системы (8.3.3) заключаем, что давление не зависит ни от  , ни от
, ни от  , а может быть функцией только
, а может быть функцией только 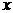 .
.
Обратимся к первому уравнению системы (8.3.3). Так как справа в уравнении стоит функция только  , а слева - функция только
, а слева - функция только 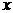 , то равенство возможно только тогда, когда правая и левая части равны некоторой постоянной величине, не зависящей от координат. Тогда имеем:
, то равенство возможно только тогда, когда правая и левая части равны некоторой постоянной величине, не зависящей от координат. Тогда имеем:
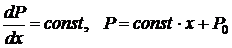 . (8.3.4)
. (8.3.4)
Здесь снова приходится обращаться к правдоподобной гипотезе о симметрии эффекта. Из (8.3.4) следует, что на бесконечности (при 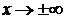 ) давление является неограниченным. Но это трудно понять физически, т. к. движение жидкости в любой точке начиналось из одного и того же состояния, не зависящего от координаты
) давление является неограниченным. Но это трудно понять физически, т. к. движение жидкости в любой точке начиналось из одного и того же состояния, не зависящего от координаты 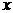 . Поэтому постоянную в уравнении (8.3.4) можно считать равной нулю. В соотношении (8.3.4)
. Поэтому постоянную в уравнении (8.3.4) можно считать равной нулю. В соотношении (8.3.4) 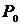 есть некоторое постоянное давление, которое можно обозначить как
есть некоторое постоянное давление, которое можно обозначить как  .
.
Тогда для нахождения распределения скорости в зазоре имеем уравнение:
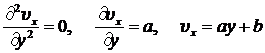 . (8.3.5)
. (8.3.5)
Граничные условия к уравнению (8.3.5) имеют вид:
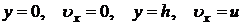 .
.
Используя граничные условия, имеем:
 . (8.3.6)
. (8.3.6)
|
.
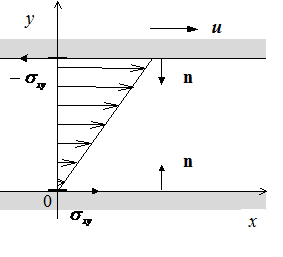
Как видно, скорость не зависит от коэффициента вязкости. На рис.8.2. изображена эпюра скоростей частиц жидкости в зазоре согласно уравнению (8.3.6).
Найдем силы, действующие на единичную площадку на поверхностей. Рассмотрим силу действующую в направлении оси 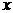 на единицу площади нижней поверхности.
на единицу площади нижней поверхности.
| Рис. 8.2 | Переобозначим для краткости |
записи тензор напряжений
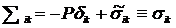 .
.
Согласно определению (п. 5.3.1) сила, действующая на единичную площадку в направлении оси 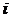 , равна:
, равна:
 .
.
Для нижней поверхности нормальный единичный вектор имеет компоненты 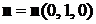 . Следовательно, для силы
. Следовательно, для силы  получим следующее выражение:
получим следующее выражение:
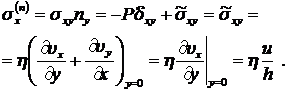 (8.3.7)
(8.3.7)
Заметим, что здесь использовано условие несжимаемости жидкости 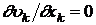 . Сила, действующая на верхнюю поверхность в направлении оси
. Сила, действующая на верхнюю поверхность в направлении оси 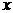 с
с 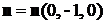 , равна:
, равна:
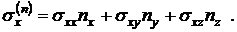
Поэтому имеем:
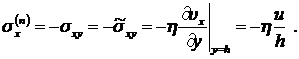
Как и следовало ожидать, силы оказались равными, но противоположно направленными.
Сила, действующая на единицу площади нижней поверхности
в направлении оси 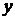 , равна
, равна

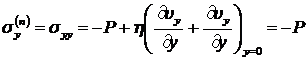 . (8.3.8)
. (8.3.8)
Легко убедиться, что на единицу поверхности верхней плоскости в направлении оси 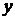 действует сила, равная
действует сила, равная  .
.
Выделим в зазоре некоторую индивидуальную частицу, имеющую форму квадрата (рис.8.3), и определим силы, действующие на стороны этого квадрата, вызываемые окружающей жидкостью. Силы, действующие на стороны, перпендикулярные оси 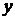 , уже определены выше, и так как они не зависят от
, уже определены выше, и так как они не зависят от 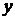 , то будут одинаковы во всех сечениях, перпендикулярных оси
, то будут одинаковы во всех сечениях, перпендикулярных оси 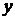 . Силы, действующие на сторону 1-2 с
. Силы, действующие на сторону 1-2 с
| Рис. 8.3 | 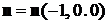 в направлении оси в направлении оси 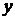
|
и x, равны соответственно:
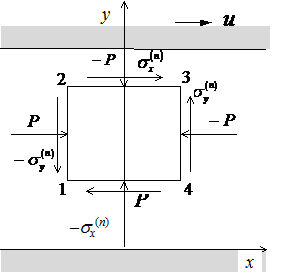
|
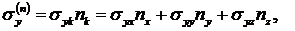
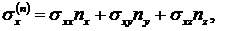
Поэтому имеем:
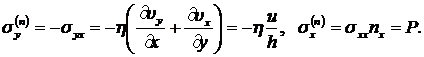 (8.3.9)
(8.3.9)
Аналогично можно показать, что силы, действующие на сторону 3-4 индивидуальной частицы (см. рис. 8.3), вследствие обратного направления нормали соответственно равны и противоположны по знаку найденным выше.
На рис.8.3 видно, что выбранная частица подвергается сжатию силами давления P и перекосу тангенциальными силами 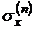 и
и 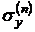 . Выше специально подробно рассмотрено нахождение всех сил, действующих на частицу, т. к. в данном случае лучше воспользоваться формальными определениями, чем полагаться на интуицию.
. Выше специально подробно рассмотрено нахождение всех сил, действующих на частицу, т. к. в данном случае лучше воспользоваться формальными определениями, чем полагаться на интуицию.
Полученное точное решение задачи Куэтта может быть использовано для экспериментального определения феноменологического коэффициента динамической вязкости h. Для этого нужно измерить силу, действующую на единицу площади верхней или нижней поверхности. Тогда, измеряя расстояние между плоскостями и воспользовавшись формулой (8.3.7), можно определить коэффициент вязкости. Однако с точки зрения экспериментальной техники это не самый простой способ измерения коэффициента динамической вязкости жидкости.
Не нашли, что искали? Воспользуйтесь поиском: