Цилиндрическое течение Пуазейля

Рассмотрим установившееся изотермическое движение вязкой несжимаемой жидкости в круглой цилиндрической неограниченно длинной трубе, вызываемое постоянным градиентом давления, который направлен вдоль оси трубы. Для решения естественно воспользоваться цилиндрической системой координат. Уравнение Навье-Стокса, уравнение непрерывности для несжимаемой жидкости, а также компоненты тензора напряжений в цилиндрической системе координат имеют вид:

,

, (8.3.15)

,

,

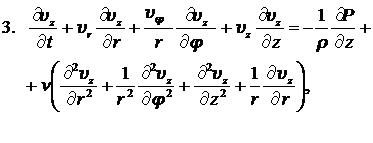Снова будем полагать, что если труба расположена горизонтально, то сила тяжести не влияет на движение жидкости в трубе. Естественно направить ось z вдоль оси трубы. Будем также полагать, используя гипотезу 2, что скорости частиц жидкости в трубе имеют единственную компоненту, направленную вдоль оси трубы и зависящую только от радиуса r. Следовательно, необходимо решить уравнение Навье-Стокса при следующих условиях:

(8.3.16)

При условиях (8.3.16) из уравнений (8.3.15) получим:

. (8.3.17)

Из первого и второго уравнения системы (8.3.17) следует, что при заданной топологии течения давление не должно зависеть ни от r, ни от j, а может быть функцией только z. Поскольку зависит только от r, то имеем:

.

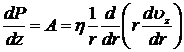После интегрирования получаем:

.

Поскольку на оси трубы не может быть бесконечной скорости, то постоянную a следует положить равной нулю. Постоянную b найдем из граничных условий:

.

Подставляя b в выражение для скорости, имеем:

. (8.3.18)

Теперь нетрудно вычислить максимальную и среднюю скорости движения жидкости по трубе.

,

.

Направления скоростей определяются направлением градиента давления.

Для объемного и массового расхода жидкости через любое сечение трубы имеем формулу Пуазейля:

. (8.3.19)

Найдем силу, действующую на единицу площади поверхности трубы в направлении оси z.

.

Используя формулы (8.3.15), имеем:

.

Вычислим силу, действующую на кольцевой элемент трубы диной D z в направлении оси z. Согласно определения силы сопротивления имеем:

.

Из последнего соотношения видно, что разность сил давлений Р ₁ и Р ₂, действующих на жидкость в двух любых сечениях трубы S ₁ и S ₂, разделенных расстоянием , уравновешивается вязкой силой, действующей на боковую поверхность рассматриваемого элемента участка трубы. Очевидно, это следует из закона Ньютона, т. к. лишь при равенстве сил рассматриваемый элемент объема жидкости будет находиться в состоянии покоя или равномерного прямолинейного движения.

Не нашли, что искали? Воспользуйтесь поиском: