Несжимаемой вязкой жидкости

Определим изменение во времени кинетической энергии движения несжимаемой вязкой жидкости за счет ее диссипации в пространстве. Рассмотрим некоторый неподвижный в пространстве объем 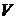, заполненный движущейся жидкостью. Кинетическая энергия жидкости в этом объеме равна

.

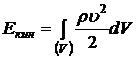Найдем изменение кинетической энергии жидкости в этом объеме в единицу времени:

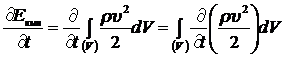. (8.2.1)

Произведем необходимые преобразования под знаком интеграла:

. (8.2.2)

Здесь первое слагаемое равно нулю, так как жидкость предполагается несжимаемой, т. е. .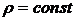

Воспользуемся далее уравнением движения Навье-Стокса для замены 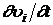в (8.2.2) и, пренебрегая действием массовых сил , получим:

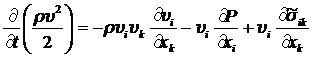. (8.2.3)

Нетрудно видеть, что слагаемые в правой части (8.2.3), используя условие несжимаемости жидкости , можно записать в виде:

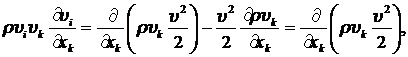
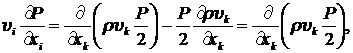(8.2.4)

.

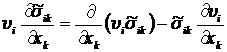После подстановки (8.2.4) в (8.2.3) и (8.2.1) имеем:

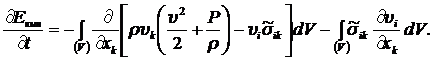(8.2.5)

Первый интеграл в правой части (8.2.5) может быть преобразован в соответствии с теоремой Гаусса-Остроградского в интеграл по поверхности , ограничивающей рассматриваемый объём. Нетрудно видеть, что выражение в квадратных скобках уравнения (8.2.5) представляет собой 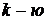компоненту вектора плотности потока энергии (вектор Умова-Пойтинга) в отсутствие потока тепла и потенциальной энергии (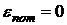). Полагая, что на бесконечно удаленной поверхности жидкость покоиться 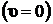, очевидно, что первый интеграл в правой части (8.2.5) равен нулю. Тогда второй интеграл в (8.2.5) определяет изменение кинетической энергии жидкости в единицу времени в рассматриваемом объёме:

(8.2.6)

Для несжимаемой жидкости 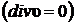тензор вязких напряжений имеет вид:

.

Поэтому выражение (8.2.6) можно записать с виде:

. (8.2.7)

Так как кинетическая энергия вязкой жидкости вследствие необратимой диссипации из-за вязкости может только уменьшаться с течением времени, то из (8.2.7) следует, что коэффициент вязкости 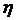всегда положителен.

Не нашли, что искали? Воспользуйтесь поиском: