Решение уравнения Навье-Стокса

Пусть неподвижный шар радиусом обтекается вязкой несжимаемой жидкостью со скорость 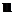на бесконечности в отсутствии внешних сил. Движение будем считать изотермическим и стационарным, тогда уравнение движения имеет вид:

. (8.4.1)

Оценим порядок слагаемых этого уравнения. Скорость набегающего потока u уменьшается до нуля на поверхности шара на расстоянии, равном приблизительно диаметру шара. Поэтому имеем:

.

Если безразмерное отношение будет значительно меньше единицы, то в уравнении движении слагаемым 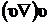можно пренебречь по сравнению с остальными слагаемыми. Это безразмерное отношение называют числом Рейнольдса (Re). Очевидно, число Рейнольдса показывает во сколько раз инерциальные силы в жидкости больше вязких сил.

Таким образом, если , то уравнение движения (8.4.1) имеет вид:

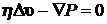. (8.4.2)

Применяя операцию rot к уравнению (8.4.2), получим:

, т. к. . (8.4.3)

Представим скорость движения частицы жидкости в виде суммы двух составляющих, т. е. , имея в виду, что добавка обращается в нуль на бесконечности. Из условия несжимаемости жидкости имеем:

, т. к. .

Поэтому добавка может быть представлена в виде т. к. . Уравнение (8.4.3) преобразуется к виду:

. (8.4.4)

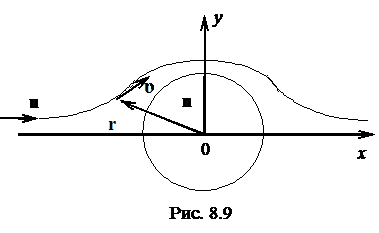
По условию задачи (рис. 8.9) имеется два полярных вектора: радиус-вектор точки наблюдения на линии тока и вектор 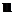скорости набегающего потока. Добавка является также полярным вектором. Поэтому вектор должен быть аксиальным вектором, т. к. ротор аксиального вектора является полярным.

Аксиальный вектор будем искать в виде

. (8.4.5)

Здесь есть произвольная функция модуля радиуса-вектора , - единичный вектор направления радиуса-вектора .

Будем искать функцию в форме производной по r некоторой функции f (r), т. е.

, . (8.4.6)

Из векторной алгебры известно, что

.

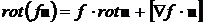Вектор скорости набегающего потока 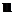постоянный, поэтому

rot(f u)=[ f · u ]. (8.4.7)

Учитывая (8.4.6), (8.4.7), вектор (8.4.5) можно записать в виде:

. (8.4.8)

После подстановки (8.4.8) в (8.4.4) имеем:

. (8.4.9)

Если воспользоваться известным соотношением из векторной алгебры вида

,

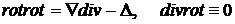то из (8.4.9) с использованием (8.4.8) следует

. (8.4.10)

Применим операцию двойного лапласиана к i -ой компоненте вектора в (8.4.10) и запишем это уравнение в тензорном виде:

(8.4.11)

Так как , то уравнение (8.4.10) можно записать в виде

. (8.4.12)

Очевидно, постоянную в правой части последнего уравнения необходимо положить равной нулю. Действительно, конечной целью решения является определение скорости как функции координат. Но согласно определения и (8.4.8) определяется только вторыми производными f по координатам, тогда как для нахождения f согласно уравнения (8.4.12) предстоит проинтегрировать f по координатам четыре раза, т. е. f будет пропорционально . Поэтому, если постоянную в (8.4.12) не полагать равной нулю, то скорость стремиться к при 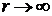, что противоречит её определению.

Тогда в сферических координатах уравнение (8.4.12) имеет вид:

.

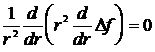Интегрируя это уравнение, получим:

. (8.4.13)

Здесь знак (-) и коэффициент 2 в константе интегрирования выбраны для удобства. По приведенным выше соображениям постоянную с также следует положить равной нулю. Следующее интегрирование приводит к результату:

(8.4.14)

При последнем интегрировании постоянная d интегрирования опущена, т. к. скорость определяется производными по координатам, поэтому постоянная интегрирования несущественна.

Не нашли, что искали? Воспользуйтесь поиском: