Плоское течение Пуазейля

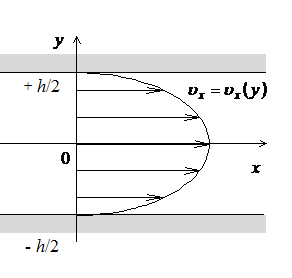
Рассмотрим бесконечные параллельные неподвижные плоскости, расстояние между которыми равно h. Пусть между плоскостями изотермически движется вязкая несжимаемая жидкость под действием постоянного градиента давления, направленного вдоль оси x (рис.8.4).

Снова будем предполагать, что если ускорение силы тяжести направлено вдоль оси y, то сила тяжести не должна влиять на движение жидкости в зазоре между плоскостями из-за малости зазора..

Пусть градиент давления создан некоторым внешним источником (насос, компрессор). Будем полагать, что движение плоское, стационарное. Снова используя гипотезу 2, будем полагать, что скорость частиц

только вдоль оси x и зависит только от y. Таким образом, необходимо решить уравнение Навье-Стокса при тех же условиях (8.3.1), что и в задаче Куэтта. Рассматривая систему уравнений (8.3.2) при сделанных предложениях, получим такие же уравнения:

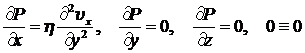. (8.3.10)

Уравнение неразрывности удовлетворяется тождественно.

Из второго и третьего уравнений следует, что давление не зависит ни от y, ни от z, а может быть функцией только x.

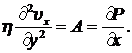
Из последнего соотношения следует, что давление P есть линейна функция x, а скорость определяется следующей формулой:

.

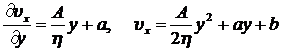Постоянные a и b могут быть определены из граничных условий:

.

Таким образом, зависимость скорости 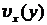можно записать в следующем виде:

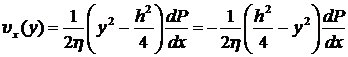. (8.3.11)

Согласно (8.3.11) эпюра скоростей (рис.8.4) представляется параболой.

Из формулы (8.3.11) легко получить среднюю 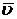и максимальную скорости течения жидкости в зазоре:

,

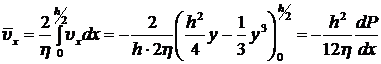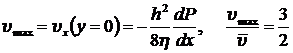. (8.3.12)

Знак скорости определяется знаком градиента давления. Если давление уменьшается вдоль оси x, то 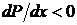, а 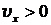, т. е. скорость направлена в сторону уменьшения давления.

Найдем силу, действующую на единицу площади верхней и нижней поверхности в направлении оси x.

,

.

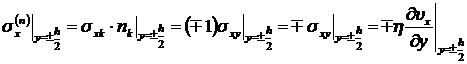Дифференцируя уравнение (8.3.11), получим:

. (8.3.13)

Как и в задаче Куэтта, сила, действующая на единичную площадкуна верхней и нижней поверхности, равна – Р и + Р, соответственно.

Объемный и массовый расходы жидкости через любое сечение, перпендикулярное оси x (единичной ширины), равны соответственно:

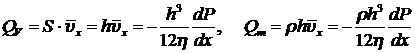. (8.3.14)

Не нашли, что искали? Воспользуйтесь поиском: