Распределение давления в поле течения около шара и

На его поверхности

Для определения силы, действующей на шар со стороны движущейся жидкости, возвратимся к исходному уравнению (8.4.2)

(8.4.19)

Согласно определению скорости она равна

.

После подстановки этого определения в (8.4.19) имеем

. (8.4.20)

Поскольку в соответствии с (8.4.12) , то из (8.4.20) следует

. (8.4.21)

После интегрирования данного уравнения по r и выбора в качестве произвольной постоянной интегрирования давления жидкости 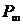в набегающем потоке вдали от шара, находим давление Р:

, (8.4.22)

но , т. к. .

Поэтому имеем

.

Принимая во внимание (8.4.13) для D f и (8.4.17) для коэффициента a, получим

,

. (8.4.23)

Формула (8.4.23) позволяет определить давление Р в любой точке r поля течения вязкой несжимаемой жидкости вблизи шара.

На поверхности шара в плоскости наибольшего его поперечного сечения распределение давления имеет вид:

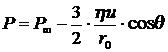. (8.4.24)

Для сравнения ниже приведены распределения по поверхности давления Р_неподв при обтекании неподвижного цилиндра потоком идеальной несжимаемой жидкости (7.6.12) и Р_двиг для двигающегося цилиндра в неподвижной идеальной жидкости (7.6.39):

.

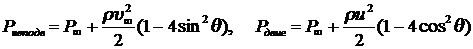Сила F, действующая на шар со стороны движущейся вязкой жидкости в общем виде и в направлении радиуса-вектора , определяется следующими интегральными соотношениями:

,

. (8.4.25)

В качестве произвольного направления действия вязкой силы удобно выбирать направление, совпадающее с направлением скорости набегающего потока 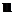. В этом случае проекции компонентов нормального единичного вектора к произвольному элементу поверхности шара dS в (8.4.25) на направление скорости набегающего потока u равны (см. рис. 8.10)

. (8.4.26)

Проекция силы F_r на направление скорости u определяет силу сопротивления шара F_u в потоке вязкой несжимаемой жидкости и в соответствии с (8.4.25, 26) она равна

.(8.4.27)

Вычислим значение компонент тензора вязких напряжений и 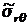на поверхности шара в сферической системе координат (8.3.14), используя соответствующие компоненты скорости и (8.4.18):

.

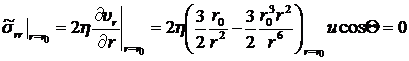Принимая во внимание, что на поверхности шара и 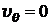, из (8.3.14) и (8.4.18) для имеем:

.

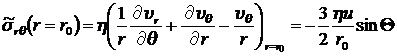После подстановки распределения давления P по поверхности шара (8.4.24) и значений и 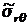в (8.4.27) получим для формулу:

.

Таким образом, при медленном обтекании шара вязкой несжимаемой жидкостью сила сопротивления равна:

. (8.4.28)

Формулу (8.4.28) называют формулой Стокса. Формула Стокса имеет широкое применение. Она используется для измерения коэффициентов вязкости жидкостей по методу падающего шарика, использовалась Милликеном при определении величины заряда электрона. Эта формула часто используется при изучении движения мелких пылинок или капель жидкости в атмосфере и т. д.

Более точное решение задачи Стокса с учетом нелинейного слагаемого 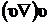в уравнении движения Навье-Стокса в области чисел Рейнольдса было получено Осееном:

(8.4.29)

Как показывает опыт, формула Осеена справедлива до чисел Рейнольдса порядка единицы. При дальнейшем увеличении числа Рейнольдса картина обтекания шара существенно изменяется (наблюдается отрыв потока с поверхности с образованием застойной зоны за шаром) и вышеприведенное рассмотрение не справедливо.

При малых числах Рейнольдса аналогичную задачу можно решить для произвольного эллипсоида и даже диска. Так для тонкого диска, расположенного перпендикулярно и параллельно набегающему потоку, сила сопротивления равна :

В системе CGS коэффициент динамической вязкости h определяют в пуазах. Один пуаз есть динамическая вязкость такой среды, в которой площадка в 1см² одного слоя испытывает со стороны другого слоя силу в 1 дину при градиенте скорости между слоями в 1 см/с на 1 см длины.

В системе СИ коэффициент h определяют в единицах, определяемых соотношением

.

Коэффициент кинематической вязкости определяется в стоксах соотношением

.

Для сведения в таблице 3.1 приведены значения коэффициентов динамической h и кинематической вязкости для некоторых сред при температуре 300К.

Следует отметить, что коэффициент динамической вязкости как газов, так и жидкостей не зависит от давления в диапазоне Р < 10 атм.

Таблица 3.1

Вещество	h,	n,
Вода	1.0×10-3	1.0×10-6
Воздух	1.8×10-5	1.5×10-5
Спирт	1.8×10-3	1.2×10-6
Глицерин	0.85	6.8×10-4
Ртуть	1.6×10-3	1.2×10-7

Динамическая вязкость газов с увеличением температуры увеличивается в соответствии с законом

.

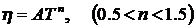Динамическая же вязкость жидкостей с увеличением температуры уменьшается. Экспериментальные данные по температурной зависимости коэффициентов динамической вязкости жидкостей хорошо описываются формулой

.

Здесь A, B и C - некоторые эмпирические константы.

Не нашли, что искали? Воспользуйтесь поиском: