
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Закон сохранения электрического заряда 1 страница
Электрический заряд не может быть уничтожен и не может быть создан. При контакте заряженных тел заряды могут только перераспределяться между телами.
 Получим математическое выражение закона сохранения электрического заряда. Рассмотрим область пространства V, окруженную замкнутой поверхностью S. Пусть в объеме V находится большое число точечных зарядов qi. Заменим истинное (дискретное) распределение зарядов непрерывным. Введем плотность заряда:
Получим математическое выражение закона сохранения электрического заряда. Рассмотрим область пространства V, окруженную замкнутой поверхностью S. Пусть в объеме V находится большое число точечных зарядов qi. Заменим истинное (дискретное) распределение зарядов непрерывным. Введем плотность заряда:
 ,
,  -радиус-вектор точки, t- время.
-радиус-вектор точки, t- время.
Полный заряд объема V:
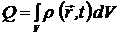 .
.
Для дискретного распределения плотность заряда:

 ,
,
где  - дельта функция Дирака. Её можно определить следующим образом:
- дельта функция Дирака. Её можно определить следующим образом:
 ,
,

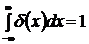 .
.
Дельта функция Дирака не обычная функция, она – представитель широкого класса обобщенных функций. Для неё имеют место следующие соотношения:
 ,
,
 .
.
Тогда:
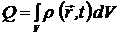 =
= 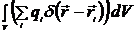 =
=  =
=  .
.
Таким образом, распределение  для дискретного распределения вполне обосновано. Для одиночного заряда q плотность
для дискретного распределения вполне обосновано. Для одиночного заряда q плотность  , где
, где  - точка нахождения заряда.
- точка нахождения заряда.
Движение электрических зарядов в пространстве – электрический ток, характеризуют вектором плотности тока

 ,
,
где  - бесконечно малый объем в окрестности точки
- бесконечно малый объем в окрестности точки  . При непрерывном распределении заряда
. При непрерывном распределении заряда
 ,
,
где  - средняя скорость зарядов в окрестности точки
- средняя скорость зарядов в окрестности точки  .
.
 Рассмотрим элементарную площадку
Рассмотрим элементарную площадку  . Тогда переносимый через площадку
. Тогда переносимый через площадку  заряд за бесконечно малый промежуток времени ∆t будет
заряд за бесконечно малый промежуток времени ∆t будет
 =
= 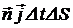 ,
,

 .
.
Выберем  . Тогда
. Тогда  , т.е. модуль
, т.е. модуль  - есть количество заряда, пересекающего за 1с единичную площадку, перпендикулярную
- есть количество заряда, пересекающего за 1с единичную площадку, перпендикулярную  .
.
Полный ток  -есть поток вектора
-есть поток вектора  через поверхность S. Величину I называют также силой тока.
через поверхность S. Величину I называют также силой тока.
Закон сохранения заряда можно записать в виде:

 .
.
Если I >0, то заряд в объеме V уменьшается.
Пусть поверхность S покоится. Тогда
 .
.
Воспользуемся теоремой Остроградского – Гаусса для полного тока
 =
=  .
.
Тогда

или
 .
.
В силу произвольности выбора объема V получим

или
 .
.
Последнее выражение называют уравнением непрерывности или законом сохранения заряда в дифференциальной форме.
1.1.3. Закон Кулона.
 Установлен Ш. Кулоном в 1785 году, а приоритет открытия закона принадлежит Кавендишу (1771 год). Закон Кулона справедлив для неподвижных точечных зарядов q1, q2 :
Установлен Ш. Кулоном в 1785 году, а приоритет открытия закона принадлежит Кавендишу (1771 год). Закон Кулона справедлив для неподвижных точечных зарядов q1, q2 :
 , где
, где  . (1.1)
. (1.1)
В гауссовой системе k=1. Размерность заряда  = абс.ед.эл.
= абс.ед.эл.
Напряженность электрического поля уединенного неподвижного заряда Q:
 . (1.2)
. (1.2)
Здесь q= q2 - пробный электрический заряд (малый положительный электрический заряд), Q= q1.Тогда из выражения (1.2) с учетом (1.1) следует:

 .
.
Размерность 
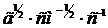 .
.
Для системы зарядов напряженность поля
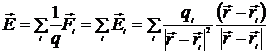 . (1.3)
. (1.3)
Соотношение (1.3) есть выражение принципа суперпозиции для напряженности электростатического поля.
 Рассчитаем поток вектора
Рассчитаем поток вектора  через замкнутую поверхность S. Поток через элементарную площадку
через замкнутую поверхность S. Поток через элементарную площадку  :
:
 .
.
 Введем телесный угол
Введем телесный угол
 ,
,  . Пусть
. Пусть 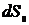 -модуль проекции площадки dS на плоскость, перпендикулярную
-модуль проекции площадки dS на плоскость, перпендикулярную  . Тогда
. Тогда
 ,
,
где функция сигнум:  .
.
 В сферической системе координат, начало которой находится в точке нахождения заряда
В сферической системе координат, начало которой находится в точке нахождения заряда  , имеем
, имеем
 . (1.4)
. (1.4)
Знак  зависит от того, какая сторона поверхности видна, т.е. определяется
зависит от того, какая сторона поверхности видна, т.е. определяется  .
.
а) Полный поток, создаваемый зарядом  внутри объема
внутри объема 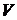 :
:
 Если в системе находится большое число зарядов, то согласно принципу суперпозиции
Если в системе находится большое число зарядов, то согласно принципу суперпозиции  имеем
имеем 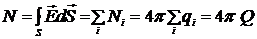 , где
, где  .
.
 Окончательно получим:
Окончательно получим:
 , (1.5)
, (1.5)
где  - полный заряд, находящийся в объеме
- полный заряд, находящийся в объеме 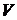 .
.
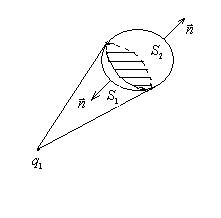
б) Заряд  находится вне объема
находится вне объема 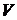 . Тогда поверхности
. Тогда поверхности  и
и  видны под одинаковым по абсолютной величине телесным углом
видны под одинаковым по абсолютной величине телесным углом  , но знаки у телесных углов разные. Таким образом,
, но знаки у телесных углов разные. Таким образом,  и
и
 . (1.6)
. (1.6)
Полный поток, создаваемый зарядами, находящимися вне объема 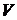 :
:
 .
.
В самом общем случае непрерывного распределения зарядов имеем:
 . (1.7)
. (1.7)
Выражение (1.7) – математическая формулировка электростатической теоремы Гаусса.
Воспользуемся теоремой Остроградского – Гаусса при вычислении первого интеграла в выражении (1.7). Тогда
 .
.
Так как последнее выражение справедливо для любого произвольного объема V, то
 . (1.8)
. (1.8)
Уравнения (1.7) и (1.8) выполняются для случая неподвижных зарядов и фактически являются другой формой записи закона Кулона. Максвелл предположил справедливость этих уравнений и в случае произвольного движения зарядов, когда  ,
,  .
.
Уравнения
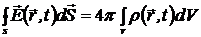 , (1.9)
, (1.9)
 (1.10)
(1.10)
были включены Максвеллом в его систему уравнений для определения электромагнитного поля при заданном законе движения зарядов.
1.1.4. Закон Био - Савара - Лапласа.
Найдем напряженность магнитного поля, создаваемого элементом с током  :
:

 . (1.11)
. (1.11)
Закон Био - Савара - Лапласа (1.11) – экспериментально установленный закон. Здесь  - электродинамическая постоянная. Размерность напряженности магнитного поля
- электродинамическая постоянная. Размерность напряженности магнитного поля  =
= 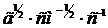 = Э (эрстед). Таким образом,
= Э (эрстед). Таким образом,
величины  и
и  измеряются в одинаковых единицах. В этом заключается основное преимущество гауссовой системы единиц перед системой СИ. Действительно, величины
измеряются в одинаковых единицах. В этом заключается основное преимущество гауссовой системы единиц перед системой СИ. Действительно, величины  и
и  являются характеристиками единого электромагнитного поля и поэтому естественно, что единицы измерения этих величин должны быть одинаковыми. Ток I в выражении (1.11) считаем постоянным, т.е.
являются характеристиками единого электромагнитного поля и поэтому естественно, что единицы измерения этих величин должны быть одинаковыми. Ток I в выражении (1.11) считаем постоянным, т.е. 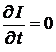 или
или  . Так как S –произвольно выбранная поверхность, то
. Так как S –произвольно выбранная поверхность, то 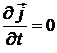 и, следовательно,
и, следовательно,  . В случае постоянного тока плотность заряда в точке не меняется из-за того, что плотность тока не зависит от времени. Таким образом, имеем
. В случае постоянного тока плотность заряда в точке не меняется из-за того, что плотность тока не зависит от времени. Таким образом, имеем 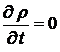 ,
, 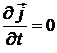 , т.е. распределение заряда – стационарно. Ток
, т.е. распределение заряда – стационарно. Ток  также будет стационарным. Из уравнения непрерывности следует, что
также будет стационарным. Из уравнения непрерывности следует, что  и
и  . Последнее означает, что поле
. Последнее означает, что поле  - соленоидальное и линии тока
- соленоидальное и линии тока  замкнуты.
замкнуты.
 Рассмотрим трубку тока (векторную трубку поля
Рассмотрим трубку тока (векторную трубку поля  ), представляющую собой поверхность, охватывающую линии тока
), представляющую собой поверхность, охватывающую линии тока  . Назовем линейным током токовую трубку, линейные размеры сечения которой, пренебрежимо малы по сравнению с расстоянием до точки наблюдения. Тогда
. Назовем линейным током токовую трубку, линейные размеры сечения которой, пренебрежимо малы по сравнению с расстоянием до точки наблюдения. Тогда

и, следовательно,
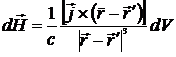 . (1.12)
. (1.12)
Найдем напряженность магнитного поля, создаваемого линейным током. Для этого проинтегрируем выражение (1.12) по объему трубки тока:
 . (1.12)
. (1.12)
Покажем, что
 =
=  .(1.13)
.(1.13)
Из (1.12) с учетом (1.13) получим
 =
=  . (1.14)
. (1.14)
Введем векторный потенциал магнитного поля
 . (1.15)
. (1.15)
Из (1.14) следует, что  . (1.16)
. (1.16)
Рассмотрим:
 =
=  =
=  .
.
Легко показать, что 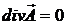 . Действительно
. Действительно
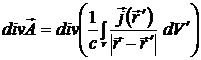 =
=  =
=  . (1.17)
. (1.17)
Учтем, что  =
= 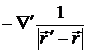 . Здесь введены обозначения
. Здесь введены обозначения  ,
,  .
.
Тогда
 =
=  =
=  .
.
Так как  , то из уравнения непрерывности
, то из уравнения непрерывности 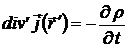 и из условия стационарности
и из условия стационарности 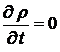 получим
получим  .
.
Следовательно
 =
=  . (1.18)
. (1.18)
Выражение (1.18) справедливо для любой поверхности S, в том числе и для бесконечно удаленной S∞, на которой  . Поэтому
. Поэтому 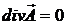 .
.
Тогда
 =
=  . (1.19)
. (1.19)
Легко показать, что
 . (1.20)
. (1.20)
Из (1.19) с учетом (1.20) получим
 =
=  =
=  .
.
Окончательно получим выражение
 =
=  , (1.21)
, (1.21)
справедливое для стационарных токов (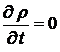 ,
, 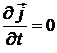 ). Его часто называют законом Ампера, что объясняется тем, что именно Ампер впервые установил всеобщую связь между магнитным полем и током.
). Его часто называют законом Ампера, что объясняется тем, что именно Ампер впервые установил всеобщую связь между магнитным полем и током.
Так как  , то
, то
 . (1.22)
. (1.22)
Действительно, 
 . Таким образом, магнитное поле
. Таким образом, магнитное поле  является соленоидальным.
является соленоидальным.
 Рассчитаем циркуляцию вектора
Рассчитаем циркуляцию вектора  по замкнутому контуру
по замкнутому контуру 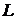 , который охватывает линии тока
, который охватывает линии тока  . На контур «натянута» поверхность
. На контур «натянута» поверхность  . Циркуляцию
. Циркуляцию  вектора
вектора  по замкнутому контуру
по замкнутому контуру 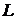 называют магнитодвижущей силой. Воспользуемся теоремой Стокса:
называют магнитодвижущей силой. Воспользуемся теоремой Стокса:
 =
=  ,
,
или
 =
=  . (1.23)
. (1.23)
Формула (1.23) выражает закон Ампера в интегральной форме. Часто этот закон называют законом полного тока.
Закон Ампера справедлив для стационарного случая, т.е.
 =
=  .
.
Для нестационарного случая, когда  и
и  , можно показать, что закон Ампера в виде
, можно показать, что закон Ампера в виде
 =
=  (1.24)
(1.24)
не выполняется. Он противоречит закону сохранения заряда в дифференциальной форме.
Действительно, из уравнения непрерывности:

в стационарном случае следует  . С учетом закона Ампера получим
. С учетом закона Ампера получим
 .
.
В нестационарном случае
 .
.
Если был бы справедлив закон Ампера в виде (1.24), то
 =
=  или
или  .
.
Таким образом, в нестационарном случае следует изменить вид уравнения (1.24) так, чтобы оно не противоречило закону сохранения заряда, являющегося одним из фундаментальных законов природы.
Обобщение закона Ампера на нестационарный случай было сделано Максвеллом. Для этого в уравнение (1.24) он добавил произвольную векторную функцию  . Тогда
. Тогда
 =
=  +
+  . (1.25)
. (1.25)
Найдем
 =
=  =
= 

или, с учетом уравнения непрерывности  , получим
, получим
 . (1.26)
. (1.26)
Из уравнений  и (1.26) следует:
и (1.26) следует:
 . (1.27)
. (1.27)
Тогда
 =
=  ,
,
где  - произвольный вектор. Максвелл предположил, что
- произвольный вектор. Максвелл предположил, что 
 .
.
Окончательно, получим обобщенный закон Ампера в виде
 =
=  +
+ 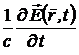 . (1.28)
. (1.28)
Это второе векторное уравнение из системы уравнений Максвелла. Оно обобщает закон Ампера и, в конечном счете, является обобщением опытного закона Био-Савара–Лапласа.
В интегральной форме уравнение (1.28) может быть записано в виде
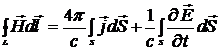 . (1.29)
. (1.29)
Максвелл ввел вектор
 (1.30)
(1.30)
и назвал его током смещения. Введение тока смещения в систему уравнений Максвелла приводит к наличию волнового решения этой системы. Электромагнитные волны, предсказанные Максвеллом, впервые были экспериментально обнаружены Герцом.
1.1.5. Закон электромагнитной индукции Фарадея.
 Опытами Фарадея было установлено, что изменение магнитного потока (потока вектора
Опытами Фарадея было установлено, что изменение магнитного потока (потока вектора  ) через любую поверхность S, ограниченную проводящим контуром L, сопровождается появлением в этом контуре электродвижущей силы (ЭДС). Математическая форма закона электромагнитной индукции Фарадея с учетом правила Ленца:
) через любую поверхность S, ограниченную проводящим контуром L, сопровождается появлением в этом контуре электродвижущей силы (ЭДС). Математическая форма закона электромагнитной индукции Фарадея с учетом правила Ленца:
 , (1.31)
, (1.31)
где  . Электродвижущая сила ε представляет собой работу, совершаемую электрическим полем по перемещению положительного единичного заряда вдоль замкнутого контура L, т.е.
. Электродвижущая сила ε представляет собой работу, совершаемую электрическим полем по перемещению положительного единичного заряда вдоль замкнутого контура L, т.е.
 . (1.32)
. (1.32)
Тогда из выражения (5.1) получим
 =
= 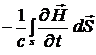 . (1.33)
. (1.33)
Замена полной производной частной возможна для случая неподвижного контура L.
Воспользуемся теоремой Стокса

или
 . (1.34)
. (1.34)
В силу произвольности выбора S из (1.34) получим
 (1.35)
(1.35)
или в интегральной форме

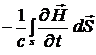 . (1.36)
. (1.36)
Уравнения (1.35) и (1.36) обобщают закон электромагнитной индукции Фарадея на случай, когда металлический контур, в котором Фарадей наблюдал индуцированный изменяющимся магнитным полем электрический ток, отсутствует. Таким образом, смысл этих уравнений заключается в том, что они устанавливают связь между магнитными и электрическими полями в любой точке пространства. Согласно (1.35) изменяющееся со временем магнитное поле порождает вихревое электрическое поле. Уравнения (1.35) и (1.36) также включают в систему уравнений Максвелла.
Не нашли, что искали? Воспользуйтесь поиском: