ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Следовательно, заряды движутся настолько медленно, что за время собственного запаздывания конфигурация зарядов не успевает заметно изменится. 3 страница

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Окончательно получим

. (7.12)

Таким образом, оставшуюся пару уравнений можно записать в виде

, (7.13)

где . Введем полностью антисимметричный тензор четвертого ранга . Определим этот тензор следующим образом. Положим ,

. Тензор называют абсолютно антисимметричным тензором Леви – Чевиты. Четное число перестановок индексов дает

элементы этого тензора равные +1, а нечетное число перестановок индексов дает элементы тензора равные -1. Всего ненулевых компонент тензора будет 4!=4·3·2·1=24.

Тогда уравнение (7.13) может быть переписано в виде

. (7.14)

Тензор - тензор третьего ранга, антисимметричный по всем трем индексам , при условии .

Таким образом, в ковариантной форме уравнения Максвелла:

(7.15)

20. Законы преобразования напряженностей поля. Инварианты электромагнитного поля.

Запишем закон преобразования тензора электромагнитного поля:

. (8.1)

Здесь

, .

Положим в (8.1) и получим

= = = .

Аналогично можно получить законы преобразования других компонент напряженностей электромагнитного поля. Окончательно имеем

(8.2)

Законы преобразования напряженностей электромагнитного поля можно записать в векторном виде. Рассмотрим параллельные и перпендикулярные к скорости компоненты векторов напряженностей электромагнитного поля, т.е. , 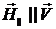и , . Тогда законы преобразования напряженностей (8.2) можно переписать в виде

(8.3)

В нерелятивистском случае 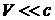эти формулы значительно упрощаются. С точностью до членов порядка получим

(8.4)

Из компонент тензора электромагнитного поля можно образовать следующие инварианты:

a) .

Выражая компоненты тензора электромагнитного поля через компоненты и , можно показать, что эти инварианты имеют вид:

(8.5)

Можно было бы образовать еще один инвариант 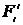. Но он тождественно обращается в нуль, т.е. .

Отметим, что первый инвариант истинный скаляр, т.е. он не изменяется как для поворотов в четырехмерном пространстве (преобразования Лоренца), так и относительно пространственных и временных отражений (преобразование инверсии). Второй инвариант псевдоскаляр. Он инвариант только для поворотов (преобразования Лоренца), но не инвариант для отражений.

Из (8.5) следует:

1) Если в какой–нибудь инерциальной системе отсчета 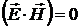, т.е. , то и в другой инерциальной системе отсчета и значит . Можно найти такую инерциальную систему отсчета, в которой либо , если , либо , если .

2) Если в какой – нибудь инерциальной системе отсчета, то они будут нулевыми во всех системах отсчета. Действительно, 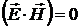и во всех инерциальных системах отсчета. Решение системы этих уравнений будет тривиальным: .

3) Если 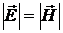в какой–нибудь инерциальной системе отсчета, то 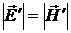во всех системах отсчета.

4) Если не перпендикулярно в какой – нибудь инерциальной системе отсчета, то можно найти такую систему отсчета, в которой .

21. Инвариантность фазы. Законы преобразования частоты и волнового вектора электромагнитной волны. Астрономическая аберрация и эффект Доплера.

Рассмотрим плоскую электромагнитную волну в инерциальной системе отсчета К:

, . (9.1)

В движущейся инерциальной системе отсчета К^':

, . (9.2)

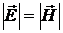В системе отсчета К имеет место: и . Следовательно,

(9.3)

Такие же соотношения будут иметь место в движущейся инерциальной системе отсчета К^':

(9.4)

Так как , то после подстановки значений из (9.1) и (9.2) получим:

,

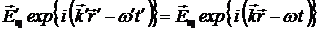или

.

Таким образом, фаза волны 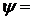- инвариант. Амплитуды волны, согласно выражениям (8.3), преобразуются по следующим правилам:

(9.5)

Введем четырехмерный контрвариантный волновой вектор и ковариантный волновой вектор . Найдем

= inv, где , .

Следовательно, и действительно являются четырехмерными векторами.

Законы преобразования четырехмерного волнового вектора можно записать в матричном виде

. (9.6)

Отсюда получим

(9.7)

В уравнениях (9.7) заключено объяснение эффекта Доплера и явления звездной аберрации.

Из волнового уравнения следует 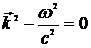. Модуль волнового вектора . Введем . Источник света покоится в системе отсчета К^', т.е. движется со скоростью относительно системы К.

Считаем, что свет распространяется в плоскости . Тогда из первого уравнения (9.7) получим

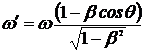, (9.8)

или

. (9.9)

Выражение (9.9) описывает эффект Доплера. Если 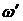- частота движущегося вдоль 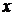источника света, то 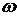- частота света, воспринимаемого покоящимся наблюдателем.

Если взять (источник света удаляется) или (источник света приближается), то из (9.9) получим

. (9.10)

Эта формула описывает продольный эффект Доплера. В нерелятивистском случае получим известную формулу эффекта Доплера:

. (9.11)

Если взять , то получим формулу для поперечного эффект Доплера

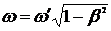. (9.12)

В нерелятивистском приближении поперечный эффект Доплера отсутствует (). В 1938 году Айвс обнаружил релятивистский эффект Доплера, т.е. эффект второго порядка по .

Из второго уравнения (9.7) получим

.

Отсюда и из выражения (9.9) получим

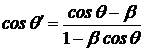. (9.13)

Согласно третьему уравнению (9.7) имеем

. (9.14)

С учетом (9.9) получим

. (9.15)

Из (9.13) и (9.15) следует известная формула

, (9.16)

объясняющая эффект астрономической аберрации.

21. Релятивистское обобщение уравнений механики Ньютона. Уравнение движения заряженной релятивистской частицы во внешнем электромагнитном поле.

Рассмотрим движение частицы в пространстве Минковского (четырехмерное псевдоевклидово пространство – время). Частица описывает в четырехмерном пространстве кривую, которая называется мировой линией.

При плоском движении частицы в коор-динатной плоскости () с постоянной скоростью 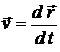мировая линия частицы –прямая линия 1 (см. рисунок). Очевидно, что , где - скорость движения частицы. Мировая линия частицы, движущейся с ускорением – кривая 2.

Траектории частиц всегда расположены внутри конуса, называемого световым конусом. Образующие этого конуса отвечают движению фотона, скорость которого равна .

Рассмотрим элемент мировой линии частицы

= , . (10.1)

Введем собственное время частицы . Очевидно, оно является инвариантом. Тогда

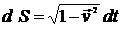. (10.2)

Обобщим понятие скорости в трехмерном пространстве на четырехмерный случай

, . (10.3)

Ковариантный вектор скорости

. (10.4)

Следует отметить, что нельзя ввести понятие четырехмерной скорости для фотона. Для четырехмерной скорости выполняется выражение

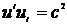. (10.5)

В нерелятивистском случае получим: , () и .

Аналогично введем четырехмерный вектор ускорения

, . (10.6)

Выражение (10.6) обобщает определение ускорения в классической механике

. Проведем расчеты и получим

. (10.7)

В нерелятивистском случае получим:

.

Из условия (10.5) получим или

. (10.8)

Таким образом, вектора скорости и ускорения ортогональны в четырехмерном пространстве.

Введем четырехмерный импульс

, = , (10.9)

где - масса покоя частица (собственная масса), являющаяся скаляром (инвариантом). В нерелятивистском случае получим:

= . (10.10)

Здесь или - обычный нерелятивистский импульс.

Если ввести так называемую релятивистскую массу

, (10.11)

которую иногда называют инертной или динамической массой, то (10.9) можно переписать в виде:

= . (10.12)

Тогда пространственную часть четырехмерного импульса можно переписать в виде

или . (10.13)

Эту часть четырехмерного импульса 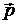называют релятивистским импульсом.

В классической ньютоновой механике уравнение движения имеет вид

. (10.14)

Минковский обобщил это уравнение на четырехмерный случай

. (10.15)

В уравнении Минковского (10.15) четырехмерный вектор 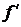называют силой Минковского.

Подставим в (10.15) значение 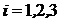, получим

, (10.16)

где релятивистский импульс . Тогда из выражения (10.16) получим уравнение:

. (10.17)

Введя релятивистскую силу , перепишем уравнение (10.17) в виде:

. (10.18)

оно обобщает нерелятивистское уравнение движения (10.14). Релятивистское уравнение движения (10.18) было предложено Пуанкаре. При условии, что , получим и . Уравнение (10.18) при этом совпадет с уравнением движения классической механики (10.14).

Рассмотрим заряженную частицу с зарядом 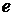, движущуюся в электромагнитном поле. На нее со стороны поля действует сила Лоренца

. (10.19)

Запишем силу Лоренца в ковариантном виде, воспользовавшись определением четырехмерной скорости и тензора электромагнитного поля:

,

.

Тогда из (10.19) получим для компоненты 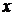силы Лоренца:

= = = .

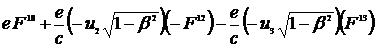Аналогично можно получить другие компоненты силы Лоренца. Их запишем в виде:

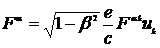, . (10.20)

Обобщим формулу (10.20), введя четырехмерный вектор силы Лоренца

. (10.21)

Отсюда сила Минковского, действующая на заряженную частицу, будет

. (10.22)

Уравнение движения заряженной частицы в электромагнитном поле (10.15) примет вид

(10.23)

или

. (10.24)

23. Законы преобразования энергии и импульса. Связь энергии, импульса и скорости релятивистской частицы.

Рассмотрим уравнение Минковского при :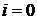

. (11.1)

Воспользуемся условием 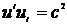, из которого следует или (). Тогда и . Подставим значение в (11.1) и получим

или

. (11.2)

Добавим к нему полученное ранее уравнение (10.18)

. (11.3)

Уравнения(11.2) и (11.3) впервые были записаны Пуанкаре.

В нерелятивистском случае () в правой части (11.2) выражение представляет мощность внешней силы. Следовательно, уравнение (11.2) примет вид:

,

где - энергия частицы. В релятивистском случае

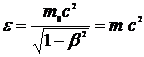(11.4)

следует считать полной энергией частицы.

Полагаем и получим из (11.4)

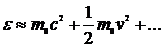. (11.5)

Здесь величина - кинетическая энергия нерелятивистской частицы, - энергия покоя частицы. В релятивистском случае кинетическую энергию частицы определим аналогично, т.е.

. (11.6)

Четырехмерный импульс частицы

= . (11.7)

Тогда

, , (11.8)

где - трехмерный релятивистский импульс. Можно записать его в виде

. (11.9)

Учтем, что

.

С другой стороны

.

Следовательно, получим выражение

,

или

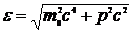, (11.10)

которое определяет связь между энергией и импульсом частицы. Скорость частицы

. (11.11)

Найдем законы преобразования энергии и импульса при переходе из одной инерциальной системы в другую

(11.12)

или

(11.13)

Здесь

Скорость || 0x, где - относительная скорость системы отсчета К^'; - скорости частиц в инерциальных системах отсчета К и К^'.

24. Принцип стационарного действия в электродинамике. Вывод уравнения релятивистской механики из принципа стационарного действия.

Рассмотрим движущийся в электромагнитном поле заряд 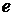. В нерелятивистском случае функция Лагранжа этого заряда

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: