Следовательно, заряды движутся настолько медленно, что за время собственного запаздывания конфигурация зарядов не успевает заметно изменится. 4 страница

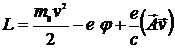. (12.1)

Введем функционал действия

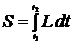, (12.2)

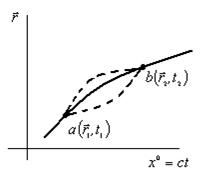
где интегрирование в выражении (12.2) проводится по некоторой кривой, соединяющей две точки (события) в четырехмерном пространстве Минковского.

Согласно принципу стационарного действия, вариация действия

.

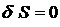Отсюда следуют уравнения движения - уравнения Лагранжа:

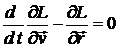, (12.3)

где , .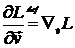

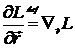Найдем обобщенный импульс системы

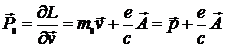, (12.4)

и обобщенную силу

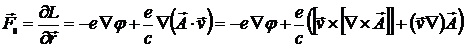. (12.5)

Из (12.3) с учетом (12.4) и (12.5) следует

=

.

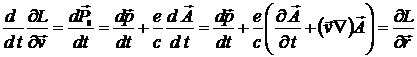Отсюда получим известное уравнение движения для нерелятивистской заряженной частицы в электромагнитном поле:

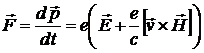. (12.6)

Получим функцию Лагранжа 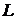для релятивистской частицы с зарядом 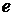, движущейся в электромагнитном поле. При этом будем руководствоваться следующими вполне очевидными положениями:

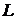· - должен быть скаляром относительно преобразований Лоренца.

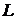· - должен зависеть только от времени, координат и скорости заряженной частицы.

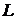· - должен иметь по возможности более простой вид и в предельном случае малых скоростей сводиться к нерелятивистской функции Лагранжа (12.1).

Для свободной частицы (в отсутствие поля) релятивистский функционал действия можно записать в виде

, (12.7)

где 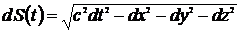- четырехмерный интервал, - некоторая постоянная. В нерелятивистском приближении функция Лагранжа

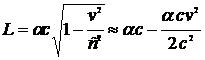. (12.8)

Если положить 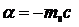, то функция 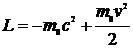сводится к нерелятивистской функции Лагранжа . Постоянная (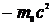) не влияет на уравнения движения частицы. Таким образом, для свободной частицы получим действие

. (12.9)

Действие для частицы, движущейся в электромагнитном поле, представим в виде

, (12.10)

где 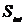- действие, описывающее взаимодействие частицы с полем. Наиболее простой вид действия

. (12.11)

Функция Лагранжа

. (12.12)

В нерелятивистском случае функция Лагранжа примет вид

, (12.13)

который совпадает с (12.1). Постоянным слагаемым (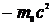) можно пренебречь, т.к. оно не сказывается на уравнениях движения.

Для вывода уравнений релятивистской механики воспользуемся принципом стационарного действия, из которого следуют уравнения Лагранжа в виде (12.3). Функцию Лагранжа (12.12) можно записать в виде:

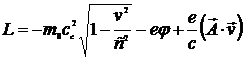. (12.14)

Проведем вычисления.

Обобщенный импульс:

,

= ,

где 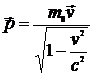- релятивистский импульс частицы. Обобщенная сила

=

=. .

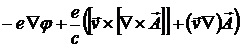Тогда

или

. (12.15)

Это известное уравнение движения Пуанкаре для релятивистской заряженной частицы в электромагнитном поле.

Легко получить второе уравнение Пуанкаре для энергии, если ввести полную энергию частицы

.

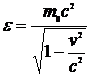Можно показать, что выполняются следующие выражения для энергии и импульса:

, .

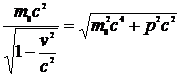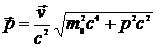Найдем

= =

= .

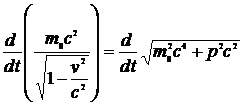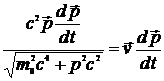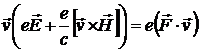Окончательно получим

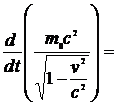
. (12.16)

Уравнения движения в гамильтоновой форме имеют вид:

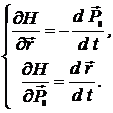(12.17)

Функция Гамильтона (энергия, выраженная через канонические координаты и импульсы)

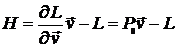, (12.18)

где функция Лагранжа

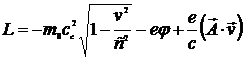, (12.19)

. (12.20)

После подстановки значений (12.19) и (12.20) в выражение (12.18) получим

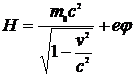. (12.21)

Функция Гамильтона как функция энергии, выраженная через координаты и импульсы, имеет следующий вид:

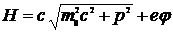. (12.22)

Вместо релятивистского импульса частицы в выражение для функции Гамильтона должен входить обобщенный импульс. Так как

,

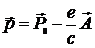то окончательный вид функции Гамильтона

. (12.23)

Воспользовавшись каноническими уравнениями Гамильтона (12.17) с функцией Гамильтона (12.23), можно получить уравнения движения заряженной частицы в электромагнитном поле (12.15) и (12.16).

25. Функция Лагранжа при заданных зарядах и токах. Получение уравнений Максвелла из принципа стационарного действия.

Запишем действие, описывающее электромагнитное поле, частицы и взаимодействие электромагнитного поля с частицами

. (13.1)

Первые два слагаемых мы уже рассматривали для случая одной частицы. Для системы невзаимодействующих частиц

. (13.2)

Действие, отвечающее за взаимодействие частиц с полем:

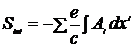. (13.3)

Перейдем к сплошной среде

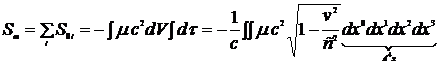, (13.4)

где 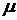- плотность массы. Выражение (13.4) перепишем в виде

. (13.5)

Здесь - лагранжиан свободных частиц, являющейся объемной плотностью функции Лагранжа . Функция Лагранжа определяется выражением

, (13.6)

и, следовательно,

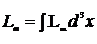. (13.7)

Таким образом, лагранжиан:

. (13.8)

Функционал действия

= = =

= .

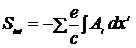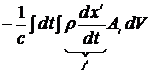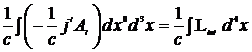Лагранжиан, описывающий взаимодействие частиц с полем

. (13.9)

Действие для электромагнитного поля

. (13.10)

Лагранжиан электромагнитного поля должен быть скаляром, т.е. комбинацией тензоров 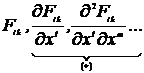. Так как уравнения электромагнитного поля не могут быть выше второго порядка, то тензоры 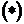не должны входить в эту комбинацию. Единственный скаляр, отвечающий этим требованиям

. (13.11)

Действие выберем в виде

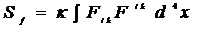. (13.12)

Лагранжиан электромагнитного поля можно записать в виде

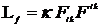. (13.13)

Для того чтобы получаемые из (13.12) и (13.13) уравнения для электромагнитного поля совпадали с уравнениями Максвелла в гауссовой системе единиц, необходимо положить 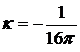. Следовательно, можно записать лагранжиан электромагнитного поля в виде

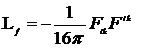. (13.14)

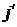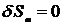Считаем, что задан закон движения зарядов, т.е. заданы и . Поэтому вариация . Будем варьировать действие

(13.15)

по компонентам четырехмерного потенциала .

Тензор электромагнитного поля

.

Вариация действия

. (13.16)

Найдем

= = = .

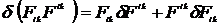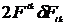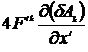Следовательно, получим для вариации действия

=

.

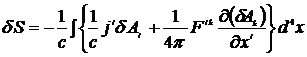Очевидно, что

, (13.17)

где - четырехмерный объем, 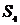- гиперповерхность в четырехмерном пространстве Минковского. На пределах интегрирования по пространственным координатам () поле исчезает, т.е. . Кроме того, на пределах интегрирования по времени вариации . Отсюда следует результат (13.17).

Окончательно для вариации действия получим

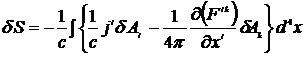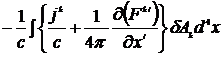= = 0.

Из-за произвольности вариации 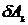из последнего соотношения следует равенство

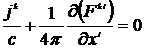
или известные уравнения Максвелла в ковариантной форме

. (13.18)

Уравнения

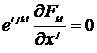(13.19)

выполняются автоматически согласно определениям тензора электромагнитного поля и абсолютно антисимметричного тензора Леви – Чевиты.

26. Тензор энергии - импульса электромагнитного поля. Плотность энергии и плотность импульса.

Рассмотрим систему заряженных частиц, находящихся в объеме 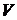. Для заряженной одиночной частицы уравнения движения в электромагнитном поле имеет вид:

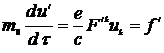. (14.1)

В случае непрерывного распределения заряда в объеме 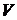плотности распределения заряда и массы 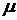связаны соотношением:

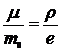. (14.2)

Следовательно, уравнение движения единицы объема

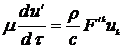
или

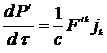, 14.3)

где 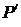- суммарный импульс единицы объема.

Воспользуемся уравнениями Максвелла (13.18) и найдем плотность тока

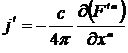. 14.4)

Тогда

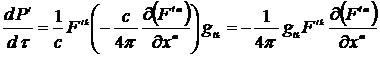. (14.5)

Представим уравнение движения в виде:

=

= =

=. .

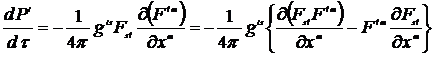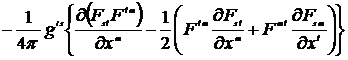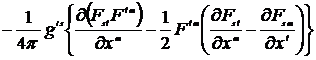Из системы уравнений Максвелла (7.13) получим

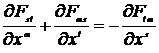или .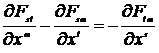

Тогда

. (14.6)

С учетом соотношения

,

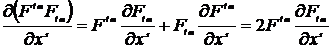из (14.6) получим

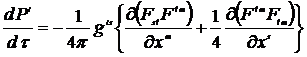
или

. (14.7)

Введем контрвариантный тензор второго ранга

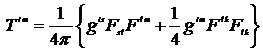, (14.8)

который называют тензором энергии – импульса. Его можно также переписать в виде

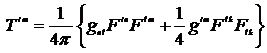. (14.9)

Тогда уравнения движения (14.7) принимают вид

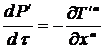. (14.10)

Отметим, что тензор энергии – импульса симметричный тензор, т.е. 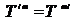. Легко заметить, что .

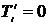Чтобы выяснить физический смысл компонент тензора энергии – импульса подсчитаем его компоненты:

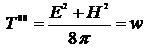· - плотность энергии электромагнитного поля.

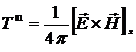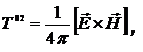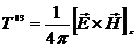· , , . Так как вектор Пойнтинга 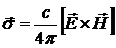, то получим для компонент тензора

, , .

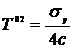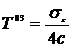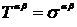· , где тензор натяжений Максвелла .

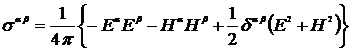Тогда тензор энергии – импульса

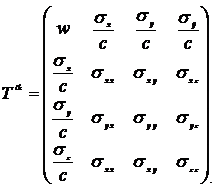
Запишем уравнение движения (14.10) в виде:

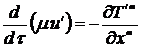. (14.11)

Рассмотрим инерциальную систему отсчета, в которой центр масс заряженных частиц покоится. Тогда

.

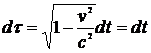Проинтегрируем (14.11) по всему объему

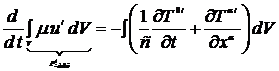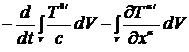= . (14.12)

Введем вектор - четырехмерный импульс электромагнитного поля в объеме 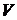. Интеграл

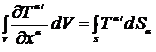
обращается в нуль для неограниченного объема.

Таким образом, из (14.12) следует

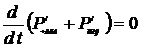. (14.13)

Выражение (14.13) представляет собой закон сохранения четырехмерного импульса системы заряженных частиц и электромагнитного поля. Электромагнитному полю необходимо приписать не только энергию 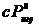, но и импульс .

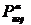Компонента четырехмерного импульса 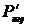при

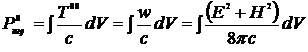. (14.14)

Плотность этой компоненты

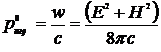. (14.15)

Положив 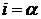, получим

или

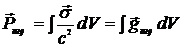. (14.16)

Плотность импульса

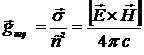. (14.17)

Рассмотрим конечный объем 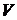, в котором отсутствуют заряженные частицы (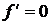). Тогда

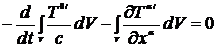
или

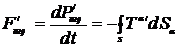. (14.18)

Последнее выражение представляет поток четырехмерного импульса поля из объема 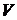через поверхность .

Положим 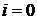. Тогда

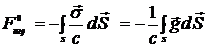. (14.19)

Для 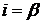из (14.18) получим

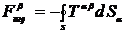. (14.20)

Рассмотрим выражение

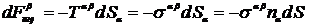. (14.21)

Отсюда следует, что тензор натяжений Максвелла 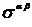представляет собой количество импульса, выходящего в направлении координатной линии через единичную площадку с нормалью . Максвелл, исходя из механических представлений об эфире, считал 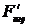- силой натяжения эфира из-за наличия в эфире электромагнитного поля.

Не нашли, что искали? Воспользуйтесь поиском: