Закон сохранения электрического заряда 3 страница

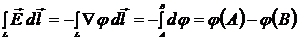
не зависит пути 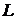. Если при положить 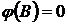, то

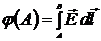. (4.8)

Найдем общее решение уравнения Пуассона (4.2). Пусть задано распределение 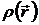во всем пространстве. Очевидно, что

.

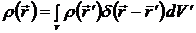Воспользуемся также соотношением

.

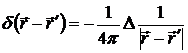Тогда

= .

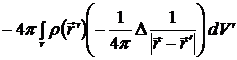Следовательно,

.

Отсюда

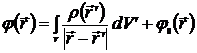, (4.9)

где 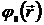- некоторое произвольное решение уравнения Лапласа

. (4.10)

Физический смысл функции 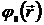заключается в том, что она определяется полем зарядов, не входящих в рассматриваемую систему. Если учесть все заряды во всем пространстве, то необходимо положить .

Таким образом, учтя распределение зарядов во всем пространстве, получим 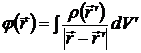, (4.11)

где интегрирование проводится по всему пространству. Выражение (4.11) – общее решение уравнения Пуассона (4.2).

Если учесть дискретный характер распределения зарядов

,

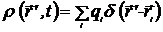то потенциал поля

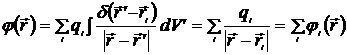. (4.12)

Последнее соотношение выражает известный принцип суперпозиции для потенциалов.

В случае распределения зарядов в конечной области пространства 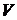необходимо для нахождения потенциала поля использовать формулу (4.9). Функция 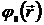удовлетворяет уравнения Лапласа

,

которое имеет однозначное решение при определенных граничных условиях на поверхности . При этом возможны три типа задач:

1. Задача Дирихле, в которой задается значение на границе .

2. Задача Неймана: Задано на границе значение производной по направлению нормали к поверхности .

3. Смешанная граничная задача: На одной части поверхности задано значение , а на другой ее части .

· Магнитостатика.

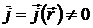Имеется система движущихся зарядов, для которой выполняются условия и . Отсюда следует 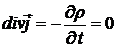, т.е. векторное поле - соленоидальное и трубки тока замкнуты.

Пусть заряды совершают финитное движение, т.е. они движутся в конечной области пространства. Покажем, что такое движение имеет стационарный характер.

Известно, что всякое финитное движение представляется либо периодическим, либо квазипериодическим и его можно характеризовать периодом

(или квазипериодом) , который является достаточно большой величиной. Пусть 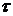постоянная прибора, которая определяется его временем срабатывания. Если 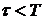, то прибор среагирует и зафиксирует измеряемую величину. В противном случае, когда 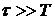прибор не успевает среагировать.

Предположим, что измеряемая величина есть ограниченная функция 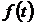. Тогда среднее значение производной от этой величины

,

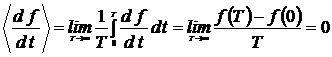из – за того, что функция () ограниченна

Таким образом, для любой ограниченной функции, относящейся к финитному движению частиц, имеем 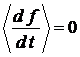. В дальнейшем будем опускать знак усреднения, т.е. вместо 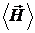писать , → и т.д.

Для магнитного поля, обусловленного финитным движением зарядов в конечной области пространства, имеем , , , 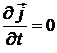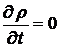. Тогда из уравнений Максвелла получим:

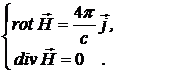
Положим и 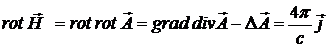. Из лоренцевской калибровки 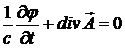получим . Следовательно,

или 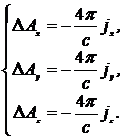(4.12)

Эти уравнения Пуассона для магнитостатики аналогичны основному уравнению электростатики

.

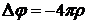Поэтому в случае, когда распределение токов задано во всем пространстве, можем решение уравнения Пуассона для магнитостатики записать в виде:

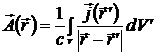. (4.13)

Последнее выражение является общим решением основного уравнения магнитостатики (4.12).

5. Векторный потенциал и магнитное поле постоянных токов. Формула Био – Савара.

Перейдем от объемных токов к линейным токам. Так как токи стационарны. . Тогда

= =

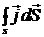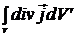или

.

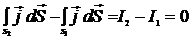Следовательно, сила тока в любом сечении трубки тока постоянна. Учтем, что , 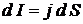. Для замкнутого линейного тока получим:

.

Окончательно получим векторный потенциал постоянного тока

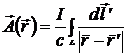. (5.1)

Подсчитаем . При расчете учтем, что . Тогда

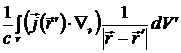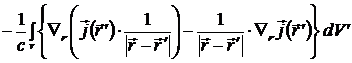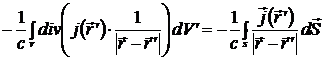= = = = = 0.

Здесь учтено, что

,

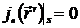так как заряженные частицы не выходят из объема проводника.

Найдем напряженность магнитного поля, создаваемого постоянными (стационарными) токами:

=

= .

Отсюда следует формула Био – Савара:

. (5.2)

Для однородного магнитного поля 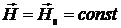векторный потенциал можно выбрать в виде

. (5.3)

Действительно,

.

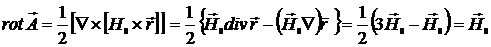6. Разложение потенциала электростатического поля по мультиполям. Электрический и квадрупольный моменты.

Предположим, что неподвижные заряды распределены в ограниченной области пространства 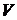по закону:

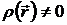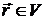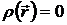при , при .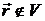

Линейные размеры системы , т.е. 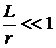и, следовательно, имеем . Таким образом, величина - малая величина.

Потенциал поля системы зарядов, распределенных в пространстве непрерывно,

. (6.1)

В случае дискретного распределения зарядов имеем

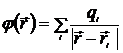. (6.2)

Напряженность поля системы зарядов

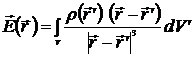или 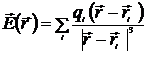. (6.3)

Воспользуемся разложением в ряд Тейлора

.

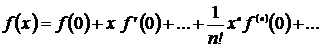В дальнейшем будем использовать тензорные обозначения:

.

Любой вектор (тензор первого ранга)

,

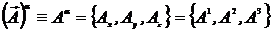Тензор второго ранга

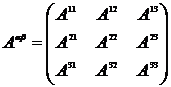, где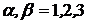

Тензор Кронекера

и .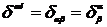

Скалярное произведение векторов

.

Здесь использовано правило суммирования Эйнштейна по повторяющимся (немым) индексам. Тогда

.

Произведем разложение в ряд Тейлора по малому параметру функции

. (6.4)

Индекс - нумерует частицы, греческие буквы – тензорные индексы. Воспользуемся свойством

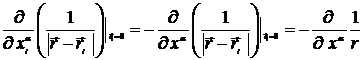. (6.5)

В этом легко убедится, положив 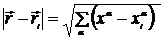. С учетом (6.5) из выражения (6.4) получим:

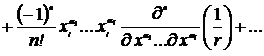. (6.6)

В векторном виде имеем

. (6.7)

Потенциал поля системы зарядов на больших расстояниях можно представить в виде:

. (6.8)

Такое представление потенциала называют разложением потенциала электростатического поля по мультиполям. В разложении (6.8) введены следующие обозначения:

,

,

.

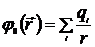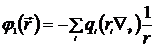Первое слагаемое в выражение (6.8) определяет монопольное приближение

, (6.9)

где 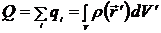- полный заряд системы. Напряженность поля в этом приближении

. (6.10)

Второе слагаемое в выражение (6.8) определяет дипольное приближение

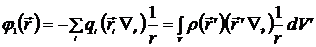. (6.11)

Так как 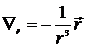, то из (6.11) следует

, (6.12)

где - электрический дипольный момент системы.

В случае электронейтральной системы полный заряд системы и . Можно показать, что для электронейтральной системы дипольный момент не зависит от выбора начала координат. Пусть , т.е. сместим начало координат на вектор 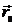. Тогда

.

В качестве примера рассмотрим систему, состоящую из двух заряженных частиц с зарядами 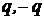. Такую систему называют электрическим диполем. Дипольный момент диполя:

, . (6.13)

Напряженность поля системы в дипольном приближении:

или

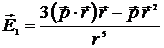. (6.14)

Cиловые линии системы в дипольном приближении найдем из системы дифференциальных уравнений:

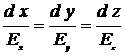. (6.15)

Картина силовых линий представлена на рисунке.

В сферических координатах решения (6.12) и (6.14) имеют вид:

, (6.16)

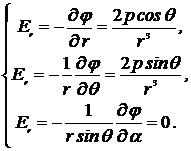(6.17)

Рассмотрим третий член разложения потенциала по мультиполям (квадрупольное приближение):

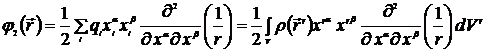. (6.18)

Введем тензор квадрупольного момента системы

(6.19)

Тогда

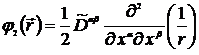. (6.20)

Вычислим вторую производную в выражении (6.20):

= = =

= =

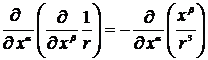Таким образом, в квадрупольном приближении потенциал поля

. (6.21)

Согласно определению (6.19), тензор квадрупольного момента системы симметричен, так что

.

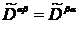Это означает, что из девяти компонент тензора только шесть являются независимыми.

Учтем, что 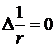при 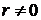. Тогда

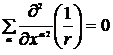или 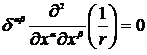. (6.22)

Перепишем (6.20), добавив в него нулевое слагаемое 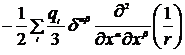. Получим:

. (6.23)

Последнее выражение позволяет выбрать тензор квадрупольного момента системы в виде

(6.24)

или

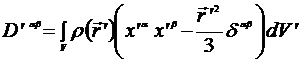. (6.25)

Легко убедится, что

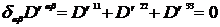. (6.26)

Соотношение (6.26) уменьшает число независимых компонент тензора квадрупольного момента до шести.

Потенциал системы

. (6.27)

Часто вводят тензор квадрупольного момента в виде

, (6.28)

и тогда потенциал системы

. (6.29)

Тензор квадрупольного момента 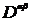- симметричный тензор. Он может быть приведен к диагональному виду

,

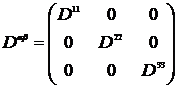где .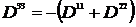

· Если симметрия сферическая (нет выделенного направления), то все .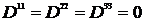

· Если симметрия аксиальная, т.е. есть выделенное направление (ось симметрии 0Z), то 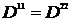и 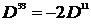. Обозначим и

В сферической системе координат в случае аксиальной симметрии

=

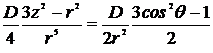= . (6.30)

Так как полином Лежандра второго порядка

,

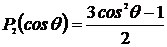то потенциал поля

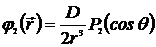. (6.31)

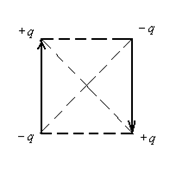Примером системы, обладающей квадрупольным моментом, является система двух диполей. Система электронейтральна, ее дипольный момент равен нулю, но квадрупольный момент .

В случае, когда 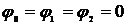, необходимо продолжить разложение. Следующий член разложения 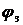- определяет октупольное приближение. Система двух квадруполей, показанная на рисунке, представляет октуполь.

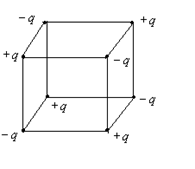
7. Энергия системы заряженных частиц. Энергия системы покоящихся зарядов в статическом внешнем поле. Силы в электростатике.

Рассмотрим систему неподвижных зарядов 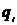. Поэтому напряженность магнитного поля и плотность энергии электромагнитного поля . Полная энергия системы зарядов

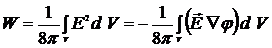(7.1)

или

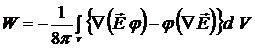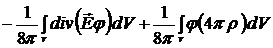= . (7.2)

Применим теорему Остроградского – Гаусса и получим

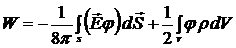. (7.3)

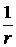Если распространить интегрирование на все пространство, то первый интеграл обращается в нуль. Действительно, при потенциал поля стремится к нулю как , напряженность поля  , площадь поверхности 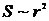 . Таким образом, при .

Окончательно получим

. (7.4)

В случае дискретного распределения зарядов полная энергия системы

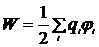. (7.5)

Так как потенциал

= ,

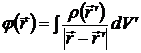то

. (7.6)

В случае дискретного распределения зарядов выделим из выражения (7.6) расходящуюся часть

, .

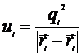Тогда

. (7.7)

Собственная энергия - того заряда 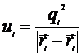. Очевидно, этот факт обусловлен тем, что заряды мы считали точечными. Если считать заряженную частицу протяженным объектом, то такой расходимости не будет.

В качестве примера рассмотрим электрон как заряженную проводящую сферу радиуса 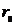и имеющую заряд 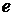. Напряженность электрического поля, создаваемого такой сферой

Тогда собственная энергия электрона

= = .

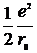Считая, что масса покоя электрона имеет электромагнитное происхождение, имеем

.

Отсюда следует, что радиус сферы 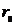, называемый классическим радиусом электрона,будет

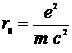. (7.8)

Расчеты показывают, что классический радиус электрона . Согласно квантовой теории, классическая теория электромагнетизма теряет смысл на расстояниях порядка комптоновской длины волны электрона . Поэтому оценка классического радиуса электрона теряет всякий смысл и проблема расходимости собственной энергии электрона может быть разрешена только в квантовой электродинамике.

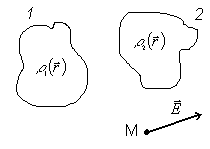Рассмотрим две удаленные системы. Рассчитаем напряженность поля , создаваемого такой системой в произвольной точке пространства M. Если известны напряженности полей 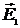и , создаваемых каждой из систем, то напряженность .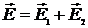

Не нашли, что искали? Воспользуйтесь поиском: