Следовательно, заряды движутся настолько медленно, что за время собственного запаздывания конфигурация зарядов не успевает заметно изменится. 1 страница

При таком условии ряд (13.10) сходится, т.е. имеет место как разложение в ряд 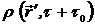, так и разложение:

. (13.12).

Проинтегрируем сходящиеся ряды (13.10) и (13.12):

{

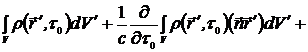
+ }, (13.13)

. (13.14)

Тогда: , где

, , ,

.

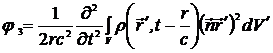Здесь 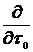заменено . Слагаемое не может быть изучением, и его отбросим, - отвечает электрическому дипольному излучению (E₁), - магнитному излучению (M₁), 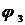- электрическому квадрупольному излучению (E₂).

Соответственно, для векторного потенциала имеем:

,

где

, ,

, .

Здесь проведена операция симметризации. Сумма:

.

Слагаемое 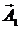описывает электрическое дипольное излучение (E₁), - магнитное излучение (M₁), 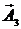- электрическое квадрупольное излучение (E₂). Названия членов разложения будет выяснено позже.

Возможны три области, в которых справедливы разложения (13.10) и (13.12).

1. Ближняя (статическая) зона: .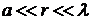

2. Промежуточная (индукционная) зона: .

3. Дальняя (волновая) зона: .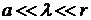

В ближней зоне поле имеет статический характер, оно пропорционально 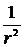и не представляет для нас особого интереса. В дальней зоне поле носит волновой характер, т.е. пропорционально .

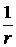14. Излучение в электрическом дипольном приближении(E1).

Рассмотрим члены разложения:

, (14.1)

(14.2)

и уравнение непрерывности:

. (14.3)

Дипольный электрический момент системы:

.

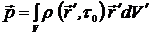Тогда

(14.4)

и потенциал

. (14.5)

С учетом (14.3) получим из (14.4):

. (14.6)

Умножим на произвольный постоянный вектор :

=

= .

Здесь учтено, что

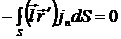, т.к. .

Таким образом, получим

. (14.7)

Тогда

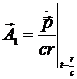, . (14.8)

Это потенциалы электрического дипольного приближения (E1). В выражения (14.8) входит дипольный момент системы. Этим объясняется название рассматриваемого приближения.

Найдём значения электрической и магнитной составляющих поля в электрическом дипольном приближении. Напряженность магнитной составляющей поля:

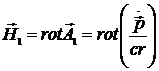= , где .

+ = =

= + .

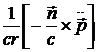Окончательно получим:

+ . (14.9)

Вторым слагаемым в (14.9) можно пренебречь, т.к. эта часть поля не в состоянии перенести энергию от источника в пространственную бесконечность. Действительно, если положить , то

~ = ~ .

В волновой зоне << 1 и поэтому последним членом можно пренебречь.

Напряженность электрической составляющей поля:

= .

Так как , то . Здесь учтено, что 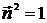. Тогда

. (14.10)

Таким образом, в электрическом дипольном приближении имеем

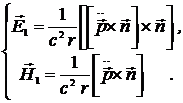(14.11)

Из (14.11) следует, что

. (14.12)

В волновой зоне имеют место следующие соотношения:

, , , , .

Волновой фронт поля излучения сферический. Действительно,

или

. (14.13)

Последнее выражение есть уравнение сферы, радиус которой растет со временем. Если при радиус сферы равен r, то в произвольный момент времени t радиус сферы станет равным .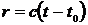

Поле излучения представляет собой сферическую электромагнитную волну, электрическая и магнитная напряженности которой с ростом убывают как .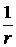

В волновой зоне

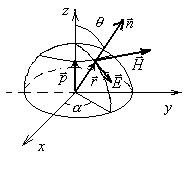Тогда

= =

= = = .

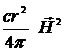С учетом (14.11) получим

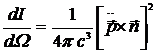, (14.14)

где - количество электромагнитной энергии, протекающей за единицу времени в единицу телесного угла. Очевидно, что

.

Вектор Пойнтинга:

,

или

= . (14.15)

Энергия излучается по направлениям неодинаково. Максимальное значение электромагнитной энергии излучается в экваториальной плоскости, т.е. при .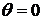

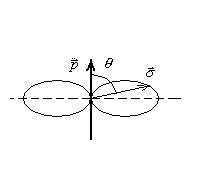Диаграмма направленности излучения представлена на рисунке.

Найдем полную интенсивность:

= =

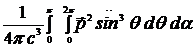
Окончательно получим

. (14.16)

Рассмотрим излучение одиночного заряда . Дипольный момент системы зарядов

.

Если в систему входит только один заряд, то . Тогда , где - ускорение заряда. Следовательно, полная интенсивность излучения движущейся заряженной частицы:

. (14.17)

Вектор Пойнтинга, определяющий плотность потока энергии излучения:

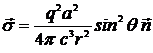. (14.18)

Так как , то при 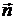заряд не излучает.

Таким образом, заряженная частица, которая движется ускоренно, излучает. При рассмотрении задачи об излучении движущегося заряда мы пользовались формулами, которыми фактически пользоваться нельзя, так как теряется смысл времени собственного запаздывания. Поэтому надо воспользоваться точным решением – потенциалами Лиенара – Вихерта. Можно показать, что при точном рассмотрении задачи получатся те же результаты (14.17), (14.18).

15. Магнитное дипольное (М1) и электрическое квадрупольное излучения (Е2).

Рассмотрим члены магнитного дипольного приближения (М1):

,, (15.1)

, (15.2)

Тогда

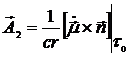, (15.3)

где магнитный момент системы:

Напряженности электрической и магнитной составляющих поля:

(15.4)

= , где .

Окончательно получим:

. (15.5)

Таким образом,

(15.6)

Все формулы для магнитного дипольного излучения (М1) могут быть получены из формул для электрического дипольного излучения (Е1) заменами:

, , .

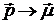Вектора 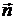, и 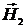образуют правую тройку.

Интенсивность излучения в единицу телесного угла:

= = ~ .

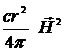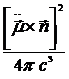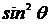Полная интенсивность:

= . (15.7)

Сравним интенсивности электрического дипольного и магнитного дипольного излучения: = . Положим 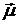, . Тогда: , . Оценим электрический и дипольный моменты:

,

.

Таким образом,

~ .

Рассмотрим следующие слагаемые, отвечающие за электрическое квадрупольное излучение (E2):

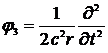
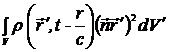, (15.8)

. (15.9)

Следовательно

, где

Учтем, что , .

Тогда: = = .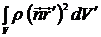

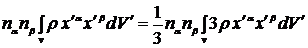Здесь введен электрический квадрупольный момент системы:

= , (15.10)

, т.е. .

Из (15.8) следует:

. (15.11)

Рассмотрим

= =

- = - .

Учтём, что = 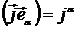. Тогда получим

.

Так как = 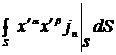, , , , то

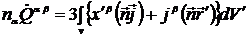(15.12)

Из (15.9) с учетом (15.12) получим:

. (15.13)

Выражение (15.13) можно переписать в векторной форме

,

где - орт β – ой координаты. Если ввести вектор 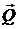с координатами , то получим:

(15.14)

Введем приведенный квадрупольный момент

= . (15.15)

В формулах (15.14) можно вместо 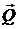поставить . Это можно осуществить, если выбрать новую калибровку:

(15.16)

где .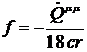

Окончательно получим:

(15.17)

Здесь учтено, что

Найдем напряженность ‘электрической и магнитной составляющих поля излучения в электрическом квадрупольном приближении (Е2):

Тогда:

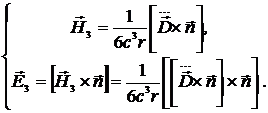(15.18)

Интенсивность излучения в единицу телесного угла:

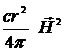= = . (15.19)

Здесь использована формула Лапласа:

,

или . Перепишем формулу (15.19) в тензорных обозначениях:

. (15.20)

Вычислим полную интенсивность излучения:

.

Согласно задаче №1.14 из методического пособия (Буйнов Н. С., Адаменко П. Г. Задачи по курсу «Электродинамика». Витебск: ВГУ, 2000 г.) имеем следующие соотношения:

(15.21)

Тогда:

. (15.22)

С учетом соотношений

,

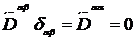(так как ),

получим из (15.22):

. (15.23)

Проведем оценки полных интенсивностей излучения. Интенсивность электрического квадрупольного излучения (E2):

.

Интенсивность магнитного дипольного приближения (М1):

.

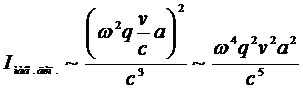Следовательно, в волновой зоне (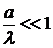) имеем:

~

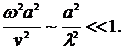
16. Сила радиационного (лучистого) трения.

Частица, двигаясь ускоренно, излучает электромагнитную энергию. Это приводит к потере импульса частицей и означает, что на частицу со стороны электромагнитного поля действует некоторая сила, получившая название силы радиационного (лучистого) трения. Само явление называется реакцией излучения. Таким образом, корректная постановка задачи о движении заряженной частицы требует включения в уравнения движения членов, учитывающих влияние излучения на движение частицы.

Рассмотрим движение нерелятивистской частицы под действием внешней силы 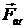. Для учета влияния радиационного трения добавим в уравнение движения силу радиационного трения . Тогда

, (16.1)

где . Так как полная энергия системы (электромагнитное поле + частица)

,

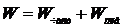то

, (16.2)

где кинетическая энергия частицы . Изменение энергии поля связано с работой силы радиационного трения , т.е.

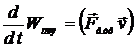. (16.3)

Излучаемая частицей в единицу времени энергия

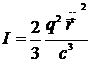
должна компенсировать работу силы радиационного трения . Однако, такая форма записи баланса энергии

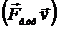= (16.4)

не верна из-за того, что и 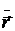заданы в разные моменты времени. Действительно, ускорение частицы через некоторый промежуток времени приводит к новому значению скорости .

Пусть частица совершает периодическое или квазипериодическое движение с периодом T. За период движения работа силы радиационного трения должна быть равной излученной энергии, т.е.

= = =

= .

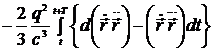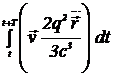Здесь учтено, что и . Таким образом, имеем

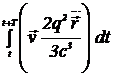= . (16.5)

В качестве силы радиационного трения можно выбрать

= = . (16.6)

Конечно из (16.5) следует, что в выражение (16.6) можно добавить слагаемое , где и - произвольные постоянные скаляр и вектор. Оно не изменит закон сохранения энергии.

Не нашли, что искали? Воспользуйтесь поиском: