Закон сохранения электрического заряда 6 страница

.

Это выражение совпадает с выражением для обычного кулоновского потенциала для момента времени . Векторный потенциал

при этом будет малой величиной.

Найдем напряженности электромагнитного поля движущегося заряда

, . (12.10)

Неудобство вычислений в выражениях (12.10) заключается в том, что запаздывающие потенциалы (12.8), (12.9) сложным образом зависят от и :

.

Продифференцируем последнее выражение по :

.

Отсюда следует

. (12.11)

Найдем

=

= .

Здесь учтено, что

.

Тогда получим

. (12.12)

Подсчитаем

= = ;

;

=

= =

= =

= ;

= =

= .

Для электрической составляющей поля получим

= , (12.13)

где

, (12.14)

, (12.15)

Все величины, зависящие от времени, в формулах (12.14), (12.15) берутся в момент времени = .

Поле 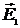зависит от скорости частицы и при поле . На больших расстояниях при поле становится кулоновским. При этом величина .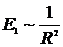

Поле зависит от ускорения частицы . При поле . На больших расстояниях , т.е. оно убывает медленнее кулоновского поля. Поле называют полем излучения заряда, движущегося с ускорением.

Для магнитной составляющей поля получим

, или 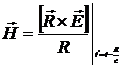. (12.16)

13. Излучение. Физические условия применимости мультипольного разложения в задаче об излучении.

В случае произвольного распределения зарядов выполнить интегрирование в формулах для запаздывающих потенциалов практически невозможно. Поэтому интегрирование проводят приближённо с помощью разложения в ряд. Мы выполнили интегрирование точно в случае одиночного заряда. На далеких расстояниях от заряда напряженность поля пропорциональна ускорению: 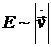или .

Для системы произвольно движущихся зарядов также в разложении на больших расстояниях будут присутствовать члены :

,

.

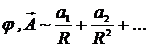Членами будем пренебрегать при условии, что .

Будем называть излучением ту часть электромагнитной энергии, которая переносится на большие расстояния (пространственная бесконечность). Другую часть электромагнитного поля можно назвать пульсацией электромагнитного поля. Излучаемую системой энергию описывают с помощью вектора Пойнтинга:

, (13.1)

который характеризует плотность потока излучения. Модуль вектора Пойнтинга -количество электромагнитной энергии, проходящей через единицу площади за единицу времени.

Интенсивность излучения (поток электромагнитной энергии) в элемент телесного угла

, . (13.2)

Тогда 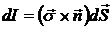, где . Так как , то 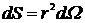. Окончательно получим

(13.3)

Таким образом, - количество энергии, протекающей за единицу времени через элемент шаровой поверхности 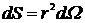с центром в начале координат.

Рассмотрим запаздывающие потенциалы:

, (13.4)

. (13.5)

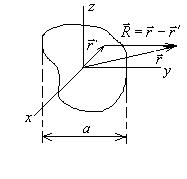Пусть a – характерный размер системы. Рассмотрим поле на больших расстояниях . Тогда - естественный малый параметр. Получим

, (13.6)

. (13.6)

Отсюда следует

, (13.7)

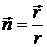, . (13.8)

Полное время запаздывания представлено в виде:

. (13.9)

Величина - время запаздывания системы, т.е. время распространения электромагнитной волны из начала координат до точки наблюдения . Второй член в разложении (13.9): - собственное (локальное) время запаздывания. По порядку величины оно совпадает с характерным временем распространения электромагнитной волны в пределах системы. В электростатике () имеем: . В нашем случае: . Введём собственное время запаздывания и . Тогда получим:

. (13.10)

Для сходимости ряда (13.10) необходимо выполнение условия 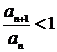, в частности, . Введем период (квазипериод) движения зарядов T. Тогда: , и Длина волны: , , и, следовательно, или . С другой стороны, скорость движения зарядов т.е.

. (13.11)

Не нашли, что искали? Воспользуйтесь поиском: