Закон сохранения электрического заряда 4 страница

Полная энергия системы

. (7.9)

Введем следующие обозначения:

- собственная энергия системы 1, - собственная энергия системы 2, - энергия взаимодействия систем.

Таким образом, полная энергия

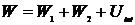. (7.10)

Преобразуем выражение для энергии взаимодействия двух систем:

= = .

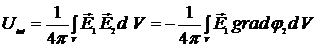Если интегрирование проводить по всему пространству, то первый интеграл обращается в нуль. Учтем, что . Тогда

. (7.11)

Так как

,

то

. (7.12)

Собственная энергия каждой из систем:

(7.13)

Рассмотрим систему заряженных частиц 1, непрерывно распределенных в пространстве с плотностью 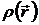. Поместим эту систему во внешнее поле , которое создается системой заряженных частиц 2. Тогда энергия системы 1 во внешнем поле будет

. (7.14)

Предположим, что первая система находится достаточно далеко от второй, т.е. . Следовательно,

(7.15)

Энергия системы зарядов

. (7.16)

Так как

, , ,

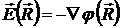то

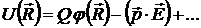. (7.17)

Обозначим через 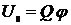энергию системы заряженных частиц во внешнем квазиоднородном поле, т.е. в поле, слабо изменяющемся в пределах системы. Это выражение можно интерпретировать как энергию точечного заряда во внешнем поле.

Если , то необходимо рассматривать второе слагаемое в разложении (7.17)

. (7.18)

Рассмотрим некоторые частные случаи.

· Энергия взаимодействия двух точечных зарядов

. (7.19)

· Энергия диполя в поле точечного заряда

. (7.20)

· Энергия диполя в поле другого диполя

,

где напряженность поля диполя

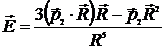. (7.21)

Тогда

. (7.22)

Найдем силу, действующую со стороны второй системы на первую

=

= . (7.23)

Момент силы, действующей на систему со стороны квазиоднородного поля

= = ,

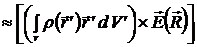т.е.

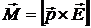. (7.24)

Пусть потенциальная энергия системы во внешнем поле , где - обобщенные координаты. При изменении координат изменение энергии будет

.

Работа, совершаемая при этом

.

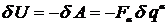Следовательно,

= .

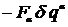Отсюда получим для обобщенной силы выражение:

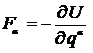. (7.25)

Если в качестве обобщенных координат выбрать , то в результате получим проекции обычной силы 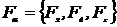. При выборе в качестве обобщенных координат угловых переменных обобщенная сила будет проекцией момента силы.

Пусть заряд находится в поле . Его энергия в этом поле . Тогда согласно формуле (7.25) получим

.

Энергия диполя в электрическом поле и сила, действующая на диполь

= .

Так как = , то

. (7.26)

Выражение (7.26) совпадает с (7.23), если положить .

В сферической системе координат .

Момент силы находим по формуле (7.25)

. (7.27)

Знак минус показывает, что момент силы уменьшает угол и диполь устанавливается вдоль поля.

В векторном виде с учетом направления момента силы формулу (7.27) можно переписать в виде

.

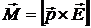Это выражение нами было получено ранее (формула (7.24)).

8. Мультипольное разложение для векторного потенциала магнитостатического поля. Дипольный магнитный момент токов. Магнитное поле в дипольном приближении.

Рассмотрим магнитное поле системы зарядов, совершающих стационарное движение в ограниченном объеме. Векторный потенциал поля

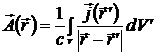, . (8.1)

Магнитное поле такой системы будем рассматривать на больших расстояниях от нее, т.е. полагаем 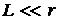или . Для дискретного распределения зарядов

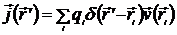. (8.2)

Подставим из (8.2) в (8.1) и получим

, . (8.3)

Воспользуемся разложением

. (8.4)

Подставим (8.4) в выражение (8.1) для векторного потенциала. Получим

. (8.5)

Покажем, что = 0 при условии стационарности: , и . Рассмотрим выражение

. (8.6)

Отсюда следует, что

.

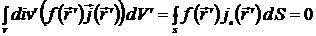Таким образом, для любой дифференцируемой функции имеет место

. (8.7)

Возьмем и подставим в (8.7). Получим

= 0 (8.8)

Если взять 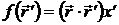, то получим

. (8.9)

Аналогично можно получить

, (8.10)

. (8.11)

Умножим обе части соотношений (8.9), (8.10), (8.11), соответственно, на орты и сложим полученные выражения. Тогда

. (8.12)

Преобразуем выражение (8.5) для векторного потенциала

= . (8.13)

Второе слагаемое выражения (8.5) вследствие (8.12) обращается в нуль, и получим

. (8.14)

Введем магнитный дипольный момент системы

. (8.15)

Тогда векторный потенциал системы

. (8.16)

В случае дискретного распределения зарядов, воспользовавшись формулой (8.2), из (8.15)

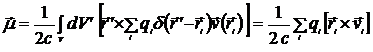. (8.17)

Последнее выражение можно переписать в виде

, (8.18)

где 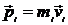- импульс частицы. Если ввести 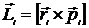момент импульса частицы (механический момент), то магнитный дипольный момент системы

, (8.19)

Можно показать, что дипольный момент не зависит от выбора начала координат. Пусть , т.е. сместим начало координат на вектор 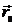. Тогда

= =

= .

Здесь учтено, что .

Рассмотрим систему частиц, у которых . Тогда

. (8.20)

Здесь введен полный механический момент системы 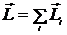. Выражение (8.20) перепишем в виде

, (8.21)

где - гиромагнитное отношение.

Подсчитаем магнитный момент линейного тока. Рассмотрим плоский контур с током .

. (8.22)

Так как

,

то

.

Тогда

.

Таким образом, магнитный момент плоского контура с током

. (8.23)

Рассчитаем напряженность магнитного поля

. (8.24)

Полученное выражение аналогично выражению для поля электрического диполя

.

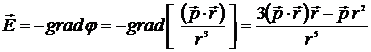Векторные (силовые) линии напряженности магнитного поля представлены на рисунке.

Рассмотрим область пространства, где отсутствуют заряды, т.е. , .

(I) (II) (8.25)

В области, где заряды отсутствуют, можно ввести псевдоскалярный потенциал магнитного поля , который определяется соотношением

. (8.26)

Действительно,

.

Таким образом, псевдоскалярный потенциал магнитного поля удовлетворяет уравнению Лапласа

. (8.27)

Решение этого уравнения можно выбрать в виде

. (8.28)

Подставим выражение (8.28) в (8.26) и получим

. (8.29)

Следовательно, в области, где заряды отсутствуют, действительно можно ввести псевдоскалярный потенциалмагнитного поля . Применение псевдоскалярного потенциала к тем областям пространства, где присутствуют заряды, приводит к неверным результатам.

9. Энергия и силы в постоянном магнитном поле.

Вычислим полную энергию ограниченной системы стационарных токов

. (9.1)

Учтем, что . Тогда

= . (9.2)

Применим теорему Остроградского – Гаусса и получим

. (9.3)

Здесь учтено, что . Если распространить интегрирование на все пространство, то первый интеграл обращается в нуль. Действительно, при векторный потенциал поля стремится к нулю как , напряженность поля  , площадь поверхности 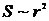 . Таким образом, при .

Окончательно получим

, (9.4)

что аналогично выражению для электростатической энергии системы покоящихся зарядов

.

Рассмотрим две удаленные системы. Напряженность магнитного поля, создаваемого такой системой, будет . Тогда полная энергия магнитного поля

. (9.5)

Тогда 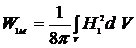- энергия системы 1, - энергия системы 2, - энергия взаимодействия систем. Преобразуем выражение для энергии взаимодействия систем

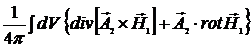= . (9.6)

Аналогично предыдущему можно показать, что

. (9.7)

Воспользуемся выражением и из (9.6) получим

. (9.8)

Пусть система 2 удалена от системы 1 на большое расстояние, т.е. . Тогда поле 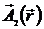, создаваемое системой 2, в пределах системы 1 слабо изменяется (поле квазиоднородное). Перейдем к координатам 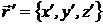, воспользовавшись соотношением . Тогда

,

и векторный потенциал

.

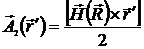Энергия взаимодействия системы с квазиоднородным магнитным полем

+

Так как 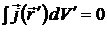, то

или окончательно получим

. (9.9)

Выражение (9.9) задает энергию взаимодействия магнитного диполя с квазиоднородным магнитным полем.

Найдем силу, действующую со стороны квазиоднородного магнитного поля, на ограниченную систему стационарных токов. Запишем силу Ампера:

и перейдем к штрихованным координатам

.

Тогда

= + .

Так как 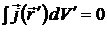, то

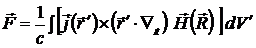. (9.10)

Рассмотрим

,

.

Здесь учтено, что . Окончательно получим

.

Следовательно,

. (9.11)

Рассмотрим

+ .

Покажем, что

.

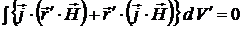Известно, что для любой дифференцируемой функции имеет место

.

Если взять , то получим

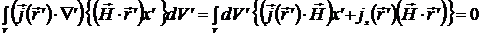. (9.12)

Аналогично можно получить

, (9.13)

. (9.14)

Умножим обе части соотношений (9.12), (9.13), (9.14), соответственно, на орты и сложим полученные выражения. Тогда

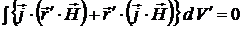. (9.15)

Таким образом, сила

=

= = ,

или

. (9.16)

Для получим

. (9.17)

Для магнитного диполя, находящегося в квазиоднородном магнитном поле, можно ввести так называемую потенциальную функцию

, (9.18)

играющую роль потенциальной энергии

для электрического диполя в электростатическом поле. Потенциальная функция . Сила, действующая на магнитный диполь в квазиоднородном магнитном поле

(9.19)

Найдем момент силы, действующей на систему

. (9.20)

Считаем поле квазиоднородным, т.е. . Тогда

.

Покажем, что второе слагаемое обращается в ноль. Рассмотрим

.

Следовательно

,

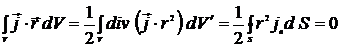так как . Получим

+ + =

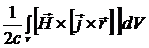
или

.

Таким образом, момент силы

. (9.21)

Если , то согласно (9.16) имеем . Однако при этом момент силы .

Пусть система состоит из одинаковых зарядов, у которых и тогда . Считаем однородное магнитное поле достаточно слабым. Наличие слабого магнитного поля приводит к медленному изменению механического момента системы, которое описывается уравнением

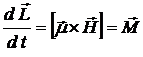. (9.22)

Учтем, что , где - гиромагнитное отношение. Тогда

, (9.23)

или

. (9.24)

Введем - ларморова частота и получим

. (9.25)

из этого уравнения следует, что вектор , а значит, и магнитный момент 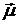вращаются с угловой скоростью . Докажем это.

Не нашли, что искали? Воспользуйтесь поиском: