Закон сохранения электрического заряда 5 страница

Рассмотрим

.

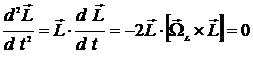Следовательно,

или .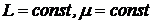

Возьмем производную от скалярного произведения :

.

С другой стороны

.

Отсюда или , . Следовательно, .

Таким образом, в слабом однородном или квазиоднородном магнитном поле система зарядов приходит во вращательное движение с угловой скоростью . Это утверждение носит название теоремы Лармора, а угловую скорость называют ларморовой частотой.

10. Электромагнитные поля при отсутствии зарядов и токов. Плоские электромагнитные волны и их свойства.

Электромагнитное поле в вакууме описывается уравнениями Максвелла при , :

(10.1)

Покажем, что не существует нетривиального (ненулевого) статического решения этой системы. В статическом случае

(10.2)

При , согласно общему решению стационарной задачи имеем

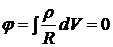. (10.3)

. (10.4)

Следовательно , , т.е. существует только нестационарное решение.

Исключим из системы уравнений (10.1) электрическую составляющую поля. Тогда

или

. (10.5)

Таким образом, нами получено однородное уравнение Даламбера: . Аналогичным образом можно получить уравнение и для электрической составляющей поля: .

Проще всего решить задачу можно, перейдя к потенциалам. Выберем . Тогда из условия Лоренца получим . Уравнение для потенциала:

. (10.6)

При этом имеем

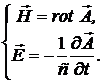(10.7)

Покажем, что есть решение , представляющее плоскую электромагнитную волну. Действительно, в фиксированный момент времени в плоскости векторный потенциал постоянен. С течением времени тоже значение будет принимать на другой плоскости .

Из условия получим . Тогда в проекции на ось 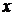уравнение для потенциала примет вид

и . (10.8)

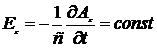Отсюда и, следовательно, . Однако постоянное поле не имеет отношение к электромагнитным волнам и может быть отброшено. Положим и . Таким образом, векторный потенциал имеет только поперечные ненулевые компоненты.

В проекции на оси получим

. (10.9)

Введем новые переменные

,

,

,

.

Тогда

. (10.10)

Его решение

, .

Следовательно

или . (10.11)

Здесь 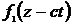- волна, распространяющаяся вдоль оси со скоростью , а 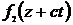- волна, распространяющаяся со скоростью в противоположном направлении.

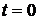Действительно, если в момент времени на плоскости , то в произвольный момент времени на плоскости . Следовательно, то же значение функция будет иметь на плоскости, отстоящей от первой на расстояние . Аналогичные рассуждения могут быть приведены и для второго слагаемого.

Рассмотрим волну , распространяющуюся вдоль оси . Тогда

. (10.12)

Так как , то . Магнитная составляющая поля

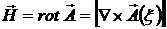. (10.13)

Отметим, что

.

Из (10.13) получим

или

. (10.14)

Таким образом, в электромагнитной волне , , 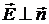. Напряженности плоских электромагнитных волн перпендикулярны к направлению распространения 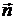и поэтому такие волны являются поперечными.

Пусть 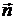направлено произвольно в пространстве относительно осей координат. Покажем, что плоская электромагнитная волна также есть решение уравнения (10.6). Действительно, если положить , то получим

или .

Фактически это означает, что выбранная форма записи есть векторная форма записи известного решения (10.11).

Рассмотрим плоскую электромагнитную волну , удовлетворяющую условию . Покажем, что . Действительно,

. (10.15)

Учтем, что и . Тогда получим

.

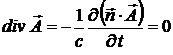Найдем производные

,

, .

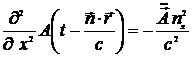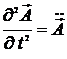Следовательно,

,

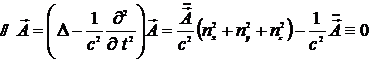т.е. - есть решение однородного уравнения Даламбера.

Тогда напряженности электрической и магнитной составляющей волны

(10.16)

Таким образом, имеем .

Перенос энергии электромагнитной волной определяется вектором Пойнтинга

. (10.17)

Так как плотность энергии , то вектор Пойнтинга

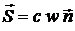. (10.18)

Таким образом, электромагнитная энергия переносится волной со скоростью света .

Пусть плоская электромагнитная волна является монохроматической. Eё можно описать с помощью векторного потенциала вида

, (10.19)

где 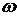- циклическая частота волны. Перепишем это выражение в комплексном виде

. (10.20)

Здесь - комплексный вектор.

Заметим, что . Если ввести обозначения: - волновой вектор, то . Следовательно, монохроматическая волна – частный случай плоской электромагнитной волны. Введем длину электромагнитной волны и тогда волновой вектор .

Очевидно, что операции дифференцирования векторного потенциала можно заменить операциями умножения по следующим правилам:

.

В случае, когда операции линейны, удобно пользоваться комплексной формой записи величин, изменяющихся по гармоническому закону. Выполнив действия с такими величинами, можно затем взять вещественную часть от полученного результата. Однако в случае, когда выполняются нелинейные операции, поступать таким образом нельзя.

Зная решения для векторного потенциала , найдем . Проведем вычисления

, (10.21)

. (10.22)

Из уравнения Максвелла 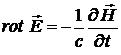получим

.

Отсюда следует

или . (10.23)

Подставим значение напряженностей в однородное уравнение Даламбера

.

Уравнение Даламбера действительно выполняется, если положить . Справедливость последнего условия очевидна, так как согласно определению волновой вектор . Аналогично можно показать справедливость уравнения .

Найдем среднее за период значение квадрата действительной части . Для этого подсчитаем

,

а затем найдем среднее за период значение

= = , где .

Таким образом, комплексная форма записи гармонически изменяющихся величин также может быть применима при вычислении среднего значения квадрата таких величин.

11. Решение уравнений для потенциалов в виде запаздывающих потенциалов.

В случае произвольно движущихся зарядов , уравнения Максвелла:

(11.1)

Его решение ищем в виде

, . (11.2)

Кроме того, дополним (11.2) условием Лоренца 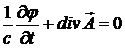. Тогда получим уравнения для потенциалов:

, (11.3)

. (11.4)

Будем искать только решение уравнения (11.3) для скалярного потенциала , так как уравнения (11.4) для проекций векторного потенциала имеет тот же самый вид.

В случае стационарного поля решение уравнения (11.3) и (11.4) известно

, (11.5)

. (11.6)

При отсутствии зарядов 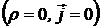получим однородное уравнение Даламбера - волновое уравнение. В общем случае уравнение для потенциалов (неоднородное уравнение Даламбера) имеет решение равное сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

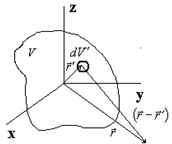
Найдем частное решение неоднородного уравнения Даламбера. Разобьем весь объем на малые области , имеющие заряд . Найдем потенциал , создаваемый таким зарядом. Выберем систему координат так, чтобы заряд находился в начале координат. Получаемое решение, конечно, не строго обосновано, так заряд изменяется со временем и тем самым нарушается закон сохранения заряда. Интегрирование по объему снимает это противоречие, и полученный результат для потенциала поля системы совпадает с точным решением.

Плотность заряда

. (11.7)

Уравнение для потенциала

. (11.8)

При имеем . Из-за сферической симметрии и в сферической системе координат получим уравнение

, (11.9)

которое может быть приведено к виду

. (11.10)

Его решение

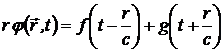, (11.11)

или

. (11.12)

Решение представляет суперпозицию сферических волн. Первая волна есть расходящаяся из начала координат сферическая волна. Вторая – сходящаяся к началу координат сферическая волна. При получим из выражения (11.12)

,

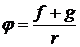которое переходит для электростатического потенциала

.

Решение можно выбрать в виде

или 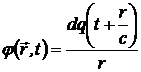(11.13).

Можно взять также в качестве решения суперпозицию этих решений. Обычно решение выбирают в виде запаздывающего потенциала , так как решение в виде опережающего потенциала не удовлетворяет условию на бесконечности в случае ограниченной системы движущихся зарядов. Действительно, только движущийся заряд создает поле, представляющее сферическую волну, распространяющуюся от заряда.

Решение в виде запаздывающего потенциала вблизи начала координат удовлетворяет закону Кулона . Условие означает, что 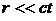. Строго говоря, это возможно, если . Тогда и уравнение (11.8) сводится к уравнению Пуассона , которое имеет решением кулоновский потенциал.

Ограничимся решением в виде запаздывающего потенциала. Скалярный потенциал, создаваемый системой зарядов

. (11.14)

Аналогично может быть записано выражение для векторного потенциала

. (11.15)

Здесь - расстояние от точки, в которой измеряется поле, до области . Тогда - время запаздывания имеет смысл промежутка времени, за которое электромагнитный сигнал распространяется от точки до точки наблюдения .

Таким образом, потенциалы (11.14), (11.15) задают электромагнитное поле в точке в момент времени , которое определяется распределением зарядов и токов в области 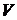в более ранние промежутки времени. Отсюда название этих потенциалов – запаздывающие потенциалы.

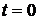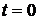Предположим, что покоящиеся заряды начинают движение в момент времени по определенному закону . Можно положить при плотности зарядов и токов , так как стационарные поля не представляют для нас интереса. При законы изменения плотностей считаем известными. Таким начальным условиям удовлетворяют только запаздывающие потенциалы. При этом можно опустить решение однородного уравнения, так как оно описывает внешнее электромагнитное поле.

Таким образом, система движущихся зарядов создает зависящее от времени электромагнитное поле – поле излучения. Легко убедиться в том, что запаздывающие потенциалы, описывающие поле излучения, удовлетворяют условию Лоренца. Действительно, получим

= = = = .

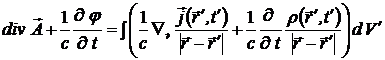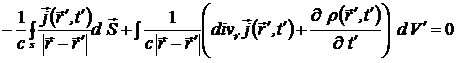Первый интеграл обращается в ноль из-за того, что на поверхности , а второй - вследствие выполнения уравнения непрерывности

.

12. Потенциалы Лиенара – Вихерта.

В выражениях для запаздывающих потенциалов

(12.1)

(12.2)

выполнить интегрирование точно практически невозможно. Единственный случай, когда такое интегрирование выполнить удается – случай произвольно движущегося заряда. Потенциалы произвольно движущегося одиночного заряда называют потенциалами Лиенара – Вихерта.

Проведем интегрирование для скалярного потенциала (12.1). Для этого запишем интеграл (12.1) в виде

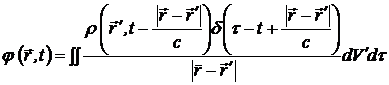. (12.3)

Плотность для одиночного заряда

.

Вначале выполним интегрирование по

=

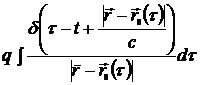=. . (12.4)

Затем выполним интегрирование по . Воспользуемся формулой

, (12.5)

Здесь

;

.

Очевидно, что , так как . Следовательно, - монотонно возрастающая функция и имеет единственный корень , который удовлетворяет уравнению:

. (12.6)

Тогда

, (12.7)

а скалярный потенциал будет

или

. (12.8)

Здесь , . Для векторного потенциала аналогичное выражение можно получить заменой :

. (12.9)

При скоростях для скалярного потенциала получим

Не нашли, что искали? Воспользуйтесь поиском: