Позначення та приклади. Міністерство освіти і науки України

Міністерство освіти і науки України

Дніпропетровський національний університет

90 – річчу ДНУ присвячується

А.В. Тушев

„ЕЛЕМЕНТИ ЗАГАЛЬНОЇ ТОПОЛОГІЇ”

Дніпропетровськ

РВВ ДНУ

ЗМІСТ

ЗМІСТ

Метричні простори.

Відкриті множини метричних просторів та їх властивості.

Топологія. Топологічні простори. Приклади.

Замкнені підмножини топологічного простору.

Внутрішні точки. Внутрішність підмножини топологічного простору.

Точки дотику. Замикання підмножин топологічного простору.

Ізольовані, граничні, межові точки.

База топологічного простору. Введення топології за допомогою бази.

Неперервне відображення топологічних просторів. Гомеоморфізми.

Компактні топологічні простори.

Список використаної літератури.

Метричні простори.

Позначення та приклади

Нехай М – множина. Метрикою, заданою на М, називається закон (правило), який кожній упорядкованій парі елементів із М ( М) ставить у відповідність деяке дійсне, невід’ємне число , причому так, що виконуються наступні аксіоми:

М1. Аксіома тотожності:

М2. Аксіома симетричності:

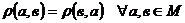
М3. Аксіома трикутника:

Таким чином, метрика 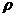на М – це відображення 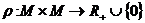, яке задовольняє аксіомам М1 – М3.

Якщо на М задана метрика 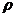, то пару називають метричним простором з метрикою .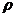

Елементи простору М називають його точками, а величину - відстанню між точками а і в.

Зазначимо, що поняття метрики узагальнює поняття відстані з Евклідової геометрії, оскільки ця відстань задовольняє означенню метрики.

Приклади:

1. На множині R введемо метрику за правилом: =| a - в |.

Аксіоми М1, М2 – очевидні. А оскільки

,

то отримали аксіому М3. Таку метрику називають природною.

1. Дискретна метрика.

Нехай М – довільна множина, введемо на М метрику наступним чином:

Аксіоми М1, М2 – очевидні з означення цієї метрики. 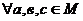розглянемо усі можливі значення метрик із співвідношення:

(*)

Якщо =0, то співвідношення (*) виконується незалежно від значень метрик у його правій частині. Якщо ж =1, то

Таким чином, 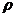- метрика на М, яку називають дискретною метрикою на М.

1. Нехай Е – п -вимірний Евклідовий простір, тобто Е – п -вимірний векторний простір над полем R, на якому введений скалярний добуток (<a,в>). За допомогою скалярного добутку вводиться довжина вектору евклідового простору

Твердження 1 (нерівність Коші-Буняковського): Нехай Е – п -вимірний Евклідовий простір, тоді .

Доведення: З аксіом скалярного добутку випливає, що для будь-яких дійсних чисел х, у виконується співвідношення:

Застосовуючи аксіоми лінійності скалярного добутку,розкриємо ліву частину цього співвідношення:

Ліва частина цього співвідношення є квадратичною формою від змінних х,у.

Оскільки , то матриця квадратичної форми (*) має вигляд:

А оскільки згідно (*), ця квадратична форма приймає тільки невід’ємні значення, то згідно критерію Сильвестра додатної визначеності квадратичної форми, виконується нерівність:

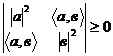
Розписуючи визначник, отримаємо:

Все доведено.

Твердження 2: Нехай Е – п -вимірний Евклідовий простір.

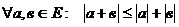
Доведення: Згідно означення довжини, маємо:

Тим самим твердження доведено.

Нехай Е – п -вимірний Евклідовий простір. Введемо на Е метрику 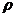наступним чином:

Покажемо, що 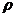задовольняє аксіоми М1-М3:

М1:

М2: М3:

Таким чином, кожен Евклідовий простір можна розглядати як метричний простір, якщо метрику на ньому ввести за правилом:

4. 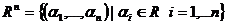- множина усіх можливих рядків довжини п з дійсними коефіцієнтами . Відомо, що 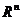- векторний простір над полем R.

Якщо операцію додавання і зовнішнього множення ввести по-координатно, крім того 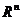є векторним простором і скалярний добуток ввести за формулою:

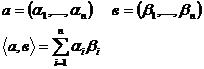
Тоді згідно приклада 3: 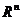- метричний простір, на якому метрика задається за формулою:

(1)

Метрику на 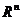, введену за формулою (1), називають Евклідовою.

5. Окрім Евклідової метрики, що була введена на 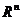за формулою (1), на цій множині можна ввести й інші метрики:

Перевіримо аксіоми метрики для :

М1:

М2:

М3:

Крім того, на 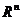можна ввести ще метрику 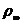за формулою:

М1:

М2:

М3:

Таким чином, на одній і тій же множині М, у загальному випадку, можна ввести багато метрик, тому позначення метрик 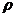у позначенні метричного простору відіграє суттєву роль: різні метричні простори. Але якщо заздалегідь відомо, про яку метрику йде мова, то метричний простір можна позначити лише символом, що позначає множину, на якій задана метрика.

6. Нехай - множина неперервних на відрізку функцій.

На цій множині можна ввести метрики, наприклад за формулою

.

Але на можна ввести й інші метрики, наприклад за такою формулою:

Не нашли, что искали? Воспользуйтесь поиском: