Замкнені підмножини топологічного простору

- топологічний простір, називається замкненою, якщо - відкрита множина.

Приклад 1:

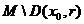- метричний простір, як було доведено раніше і - відкриті множини, тому множини та є множинами замкненими

.

Приклад 2:

У дискретній топології замкненими будуть усі підмножини, оскільки в ній всі підмножини відкриті.

Приклад 3:

У топології скінченних доповнень, задані на нескінченній множині Т (топології Заріського) замкненими будуть та усі скінченні підмножини з Т.

Теорема 1 (властивості замкнених підмножин):

Нехай - топологічний простір. -сукупність усіх замкнених підмножин цього простору, тоді має наступні властивості:

1.

2. Перетин будь-якої сукупності замкнених підмножин з Т є підмножина замкнена.

3. Об’єднання будь-якої скінченної сукупності замкнених підмножин з Т є підмножина замкнена.

Доведення: 1. Оскільки - відкриті, то - замкнені.

2. Нехай

За законами де-Моргана:

- відкрита

F – замкнена множина.

3.

За законами де-Моргана:

- відкриті

F – замкнена множина.

Що і треба було довести.

Зауваження: Об’єднання нескінченної сукупності замкнених підмножин топологічного простору у загальному випадку може бути незамкненим.

Доведення: Розглянемо на

Тоді - замкнені підмножини з R.

Кожне число, яке належить [0, 2) потрапляє в деяку множину для досить великого n, а число 2 не попадає в жодну з

, що не є замкненою підмножиною, оскільки її доповнення не є відкритою.

Теорема 2 (про введення топології за допомогою системи замкнених підмножин):

Нехай Т – деяка множина, , що задовольняє вимогам (1)-(3) попередньої теореми, тоді на множині Т існує топологія , для якої є системою замкнених підмножин.

Доведення: Нехай

Покажемо, що - топологія на Т. Перевіримо аксіоми топології:

Т1:

Т2:

Т3:

- топологія на Т.

Оскільки з означення випливає, що

- сукупність замкнених підмножин .

Внутрішні точки.

Не нашли, что искали? Воспользуйтесь поиском: