Неперервне відображення топологічних просторів. Гомеоморфізми

Нехай X, Y - топологічні простори. Відображення називається неперервним в точці , якщо .

Якщо відображення - неперервне в , то воно називається неперервним відображенням топологічних просторів.

Нехай - деяка база простору Х, - деяка база простору Y. Означення неперервності відображення можна ввести, використовуючи тільки елементи баз цих просторів, а саме:

Твердження 1: Нехай X, Y - топологічні простори, , - їх бази. Відображення буде неперервним в тоді і тільки тоді, коли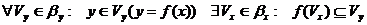

Доведення: Припустимо, що - неперервне в точці х. Виберемо

Оскільки - окіл точки у, то за означенням неперервності .

За критерієм бази .

Припустимо тепер, що відображення задовольняє умову твердження, тобто відображення – неперервне:

.

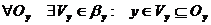За умовою твердження:

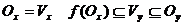Оскільки є околом точки х, то . Все доведено.

Розглянемо тепер неперервні відображення метричних просторів.

Оскільки сукупність усіх -околів метричного простору утворює базу його топології, то можна ввести наступні означення неперервності відображень метричних просторів.

Нехай X, Y - метричні простори, , . Відображення називається неперервним в точці х, якщо:

.

Оскільки і є елементами бази просторів X, Y, то згідно твердження 1, це означає еквівалентне означенню неперервності відображення топологічних просторів. В окремому випадку числових функцій (функцій, заданих на просторі R) означення неперервності має наступний вигляд:

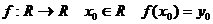
Функція f неперервна в точці , якщо:

Твердження 2 (критерій неперервності відображень топологічних просторів):

Нехай X, Y - топологічні простори, неперервне тоді і тільки тоді, коли:

1. Прообраз будь-якої відкритої множини з Y є відкритою множиною в X.
2. Прообраз будь-якої замкненої множини з Y є замкненою множиною в X.

Доведення: 1. Припустимо, що є неперервним. Нехай U – довільна відкрита множина з Y. Покажемо, що є відкритою множиною в X.

Нехай , тоді U можна розглядати як деякий окіл точки у і за означенням неперервності відображення .

Довільний х входить в V разом з деяким своїм околом є відкритою.

Припустимо тепер, що відображення задовольняє умові твердження, тобто прообраз будь-якої відкритої множини з Y є відкритою множиною в X.

Покажемо, що є неперервним, , .

Нехай - деякий окіл точки у. Оскільки - відкрита множина, то, згідно умові твердження, її прообраз є відкрита множина в X. Оскільки , то є околом точки х.

З означення неперервності 1) умова доведена.

2. Це твердження випливає з твердження 1 і рівності . Припустимо, що прообраз будь-якої замкненої множини з Y є замкненою множиною в X. Нехай V – довільна відкрита множина з Y, тоді - деяка замкнена множина. Оскільки - замкнена множина в X, то з рівності випливає, що - відкрита множина в X. Прообраз будь-якої відкритої множини з Y є відкритою множиною в X., тому - неперервне відображення. Припустимо тепер, що

- неперервне відображення, тоді з п.1) випливає, що прообраз будь-якої відкритої множини з Y є відкритою множиною в X.

Нехай V – деяка замкнена множина з Y, тоді де U – деяка відкрита множина з Y. Оскільки - відкрита множина в X, то з рівності випливає, що замкнена множина в X.

Отже, все доведено.

Твердження 3: Композиція (суперпозиція) неперервних відображень топологічних просторів є неперервним відображенням, тобто, якщо X, Y, Z – топологічні простори, і - їх неперервні відображення, то 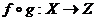є неперервним відображенням топологічних просторів.

Доведення: Застосуємо критерій з попереднього твердження:

Нехай U – довільна відкрита множина з Z, оскільки прообраз U такий що: і f, g – неперервні відображення, то згідно попереднього твердження множина - відкрита в X, а є неперервним. І все доведено.

Нехай X, Y – топологічні простори. Відображення називається гомеоморфізмом, якщо f – бієктивне, неперервне і зворотне до нього відображення.

також є неперервним.

Якщо між просторами X та Y існує гомеоморфізм, то такі простори називаються гомеоморфними і позначаються так: .

Нехай X, Y – топологічні простори. Відображення називається:

1) відкритим, якщо образ будь-якої відкритої множини є відкритою множиною в Y.

2) замкненим, якщо образ 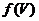будь-якої замкненої множини з X є замкненою множиною в Y.

Твердження 4: Нехай X, Y – топологічні простори, бієктивне неперервне відображення є гомеоморфізмом тоді і тільки тоді, коли воно є відкритим (замкненим).

Доведення: Доведемо твердження для відкритих відображень. Для цього застосуємо критерій (1) з твердження 3. Припустимо, що f – гомеоморфізм, і покажемо, що f – відкрите відображення. Оскільки f – гомеоморфізм, то є неперервним. Покажемо, що f(U) - відкрита множина в Y. Оскільки - неперервне відображення і f(U) – прообраз множини U при дії неперервного відображення , то згідно твердження 3 f(U) – відкрита множина в Y.

Припустимо тепер, що відображення f – відкрите і покажемо, що f – гомеоморфізм. Для цього достатньо показати, що зворотне відображення є неперервним.

Нехай U – деяка довільна відкрита множина з X, тоді f(U) є прообразом множини U при дії відображення , а оскільки відображення f – відкрите, то множина f(U) є відкритою множиною в Y.

Таким чином, згідно критерію 1 твердження 3 відображення є неперервним.

Для замкнених відображень твердження доводиться аналогічно, замість критерію 1 треба застосувати критерій 2.

Наслідок: Якщо між топологічними просторами X, Y існує гомеоморфізм , то для довільної множини виконуються співвідношення:

1.

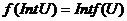
2.

3.

Якщо між топологічними просторами існує гомеоморфізм, то вони мають однакові топологічні властивості. У загальній топології гомеоморфні простори вважаються однаковими.

Твердження 5: Гомеоморфність є співвідношенням еквівалентності на класі усіх топологічних просторів, тобто:

1.

2.

3.

Доведення: 1. Якщо , то гомеоморфізм встановлює тотожне відображення.

2. Якщо - гомеоморфізм, то також гомеоморфізм.

3. Нехай - гомеоморфізм, - теж гомеоморфізм, оскільки композиція бієктивного відображення є бієктивним відображенням, композиція неперервного відображення є неперервним відображенням, зворотне до композиції є 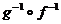, то відображення - неперервне, а відображення - гомеоморфізм. І все доведено.

Сукупність усіх топологічних просторів розпадається на класи гомеоморфних просторів і вони не перетинаються. Ці класи називаються топологічними типами. Гомеоморфні простори мають однакові топологічні типи.

Не нашли, что искали? Воспользуйтесь поиском: