Внутрішність підмножини топологічного

Простору

Т – топологічний простір, Довільна відкрита підмножина з Т, що містить А називається (відкритим) околом множини А.

Нехай Т – топологічний простір, Точка називається внутрішньою точкою А, якщо .

Сукупність усіх внутрішніх точок множини А називають внутрішністю цієї множини (Int A)

Твердження 1: Нехай Т – топологічний простір, Тоді Int A співпадає з об’єднанням усіх відкритих підмножин, що містяться в А.

Доведення: Нехай U – об’єднання усіх відкритих підмножин, що містяться в А, тоді U - також відкрита множина, що міститься в А.

Для довільного 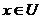: U можна розглядати як окіл точки х, з яким х входить в А, тому х – внутрішня точка з А.

Покажемо, що .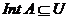

Нехай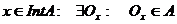

можна розглядати як окіл точки у, з яким у входить в А, тому у – внутрішня точка множини А

Таким чином, IntA є об’єднанням деякої сукупності відкритих підмножин з А, тому .

Наслідок 1: IntA є найбільшою відкритою підмножиною, що міститься в А.

Доведення: Нехай U – найбільша відкрита підмножина, що міститься в А. Оскільки IntA – відкрита підмножина з А (як об’єднання відкритих підмножин з А), то IntA міститься в U.

Але IntA – об’єднання усіх відкритих підмножин з А .

Наслідок 2: Множина А є відкритою тоді і тільки тоді, коли А=IntA.

Доведення: Якщо підмножина А – відкрита, то А і буде найбільшою відкритою підмножиною з А, тому А=IntA.

Якщо ж А=IntA, то А буде відкритою підмножиною, оскільки IntA – відкрита підмножина.

Приклад 1: Розглянемо простір R, тоді Int [a, b]=(a, b)

Приклад 2: Розглянемо R, . Оскільки будь-який відкритий окіл як раціональні, так і ірраціональні числа, то

Не нашли, что искали? Воспользуйтесь поиском: